|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Regular Articles Vol. 10, No. 11, pp. 70–78, Nov. 2012. https://doi.org/10.53829/ntr201211ra2 On the Security of the Cryptographic Mask Generation Functions Standardized by ANSI, IEEE, ISO/IEC, and NISTAbstractWe revisit the security of mask generation functions (MGFs) in light of the indifferentiability framework. MGFs are a kind of hash function having variably long outputs and they are frequently utilized for designing public-key cryptographic schemes such as digital signatures. First, we clarify that there are weak and strong versions of indifferentiability, depending on the order of quantifies in the definition. Next, we prove that the classical, counter-based MGF standardized by ANSI, IEEE, and ISO/IEC satisfies only the weak version of indifferentiability, whereas the Double-Pipeline Iteration Mode specified in SP800-108 by the National Institute of Standards and Technology (NIST) satisfies the strong version. While our analysis does not necessarily imply that counter-based MGFs are insecure, our results show that MGF constructions have different levels of security (i.e., indifferentiability). 1. Introduction1.1 BackgroundEver since its establishment by Bellare and Rogaway [1], the notion of random oracles has played an essential role in the design of asymmetric cryptographic schemes [2], [3]. Informally, random oracles are objects that should behave like public random functions, accepting variable input length (VIL) data and returning variable output length (VOL) random strings. Random oracles are ideal objects: they cannot be implemented without additional assumptions. In practice, random oracles are replaced with concrete functions. It is not an easy task to construct a random-looking VIL-VOL concrete function from scratch. So we usually start with a small concrete function that is restricted to a fixed input length (FIL) and fixed output length (FOL). Such functions are often called compression functions. We then iterate the compression functions in some way to obtain VIL and/or VOL functions. Concrete functions that accept VIL strings but return only FOL strings are commonly called hash functions. The construction of secure hash functions has been theoretically investigated in various ways. In particular, the security of hash functions as VIL (but FOL) random oracles was studied by Coron et al. [4], where the underlying compression functions were modeled as FIL-FOL (restricted) random oracles in light of the indifferentiability framework [5]. Subsequent to the work reported in [4], the domain extension of random oracles has been analyzed in depth [6]–[11]. On the other hand, the range extension of random oracles has attracted less attention from the theoretical aspect. Despite the lack of formal treatment, VOL random oracles are regularly used in designing public-key cryptographic schemes, in particular digital signatures [3]. For the random oracles utilized in those signature schemes, which achieve full message recovery [12]–[16], the variability in output length becomes absolutely crucial. There already exist several constructions for VIL-VOL concrete functions. They are called by the common name mask generation functions (MGFs). The majority of existing MGFs follow the counter-based design and have been standardized by ANSI (American National Standards Institute), IEEE (Institute of Electrical and Electronics Engineers), and ISO/IEC (International Organization for Standardization, International Electrotechnical Commission). For example, the algorithm MGF1 [13], [17]–[19] takes a hash function H: {0, 1}*→ {0, 1}n, computes upon input x the string H (x||⟨0⟩32) || H (x||⟨1⟩32) || H (x||⟨2⟩32) || ···, and truncates this string to the leftmost l bits, where ⟨i⟩α denotes an α-bit representation of integer i and l denotes the requested length. The main motivation behind the current work is to provide a formal security analysis for this type of construction. The same types of algorithms are often called key derivation functions (KDFs), mostly when they take secret inputs. These are standardized in SP800-108 by NIST (National Institute of Standards and Technology) [20]. The security of KDFs is formally treated in [21]. We analyze the security of the Double-Pipeline Iteration Mode specified in SP800-108 as an MGF that takes only public inputs. 1.2 Our resultsWe take the systematic approach proposed by Coron et al. [4] and apply the indifferentiability framework [5] to our study of MGFs. That is, we consider two MGF constructions whose security is analyzed under the condition that an ideal hash function (a VIL/FOL random oracle) H: {0, 1}*→ {0, 1}n is given. Using this basic strategy, we obtain the following results, which are summarized in Table 1:
- Local vs. universal. We point out that in the literature there are two different versions of indifferentiability notions. - Analysis of counter-based MGFs. We obtain two impossibility results for the counter-based MGF1. The first result says that MGF1 cannot be proven to be indifferentiable from the ideal MGF in the sense that there exist no natural simulators. The second result says that MGF1 itself cannot be proven to be insecure in the sense that there exists no strong adversary. - Analysis of chained MGFs. We analyze the security of the Double-Pipeline Iteration Mode specified in NIST SP800-108, which can be shown to be indifferentiable from an ideal MGF. We provide concrete security bounds for the Double-Pipeline Iteration Mode. Unlike the case of domain extension, the security of this scheme degrades only linearly with the number of oracle queries*1. 1.3 OrganizationSection 2 defines our notation and provides other preliminaries. Section 3 reviews the notion of indifferentiability, identifies a class of natural simulators, and defines an MGF. Section 4 defines the counter-based MGF and analyzes its security. Section 5 defines the Double-Pipeline Iteration Mode and analyzes its security. Section 6 concludes with a brief summary and some concluding remarks about future work.
2. Preliminaries2.1 Basic notation{0, 1}m denotes the set of bit strings whose length is equal to m > 0. {0, 1}0 denotes the set consisting of only the null string ε. {0, 1}* denotes the set of finite bit strings. |x| denotes the bit length of a string x ∈ {0, 1}*. [x]m represents the leftmost m bits of a string x ∈ {0, 1}*. [x]m represents the rightmost m bits. Given two strings x and y, we let x||y be the concatenation of x and y.
We write N for the set of positive integers and write Z≥0 for the set of nonnegative integers. By writing x ∈U X, we mean that x is an element chosen uniformly at random from the set X. 2.2 Security parameters and length encodingA security parameter is a positive integer κ ∈ N. It is customary to write 1κ ∈ {0, 1}* instead of κ ∈ N to emphasize the fact that κ is a security parameter. Whenever possible, we omit the security parameter κ and make it implicit in our statements. 2.3 Oracle machinesThroughout the paper, the computation model is fixed. Specifically, we regard any probabilistic algorithm as a (probabilistic) Turing machine. We consider an oracle machine, which is a Turing machine given access to an oracle. Interaction with an oracle is done via the machine’s communication tape, and a reply from an oracle is given immediately, i.e., the time for interaction is 1 (unit time) irrespective of the query length, the reply length, and the oracle’s behavior. Note, however, that the machine consumes the time taken to write its query onto the communication tape. Moreover, if the machine wants to read partially or wholly the reply written on the tape, the corresponding amount of time is consumed. We write A 2.4 Modes and distinguishersA mode is a deterministic algorithm M that takes as its input a security parameter 1κ and a finite string
x ∈ X, where domain X is a subset of {0, 1}*, and computes as its output a finite string y ∈ {0, 1}*. A mode M has access to an oracle A distinguisher is a probabilistic algorithm D that takes as its input a security parameter 1κ and outputs a bit b ∈ {0, 1}. A distinguisher D is given access to multiple oracles, and one of them is frequently mode M. In such a setting, we say that “the distinguisher D attacks the mode M.” Succinctly written, b ← 2.5 Time and query complexitiesGenerally speaking, we may want to restrict the capacity of an oracle machine in terms of its time complexity and query complexity. In the present work, however, we treat only query complexity because an oracle machine’s running time is irrelevant to the context of our security analysis*2. The query complexity is measured in terms of two quantities qA and lA for a given oracle machine A, where qA represents the limit on the total number of queries that machine A can send to its oracles and lA represents the limit on the maximum length of each query or reply. A construction F is said to be tractable if its bounds qF and lF are polynomials in the following three variables: security parameter κ, input length |x|, and output length |y|. A distinguisher D is said to be efficient if its bounds qD and lD are polynomials in the security parameter κ. A simulator S is said to be efficient if its bounds qS and lS, as well as the size |σ’| of updated state σ’, are polynomials in the following four variables: security parameter κ, input state length |σ|, input length |x|, and output length |y|.
3. Indifferentiability framework and security of the MGFIn this section, we revisit the notion of indifferentiability. There are two points that we would like to clarify: (1) the definition of a simulator and (2) the order of quantifiers with respect to the simulator. Now, we define the security of the MGF. 3.1 Simulator division and connector extractionIn order to define indifferentiability, we need to introduce a simulator. A simulator S is a probabilistic algorithm that takes as its input a security parameter 1κ, current state information σ ∈ Σ(where the set Σ of state information is a subset of {0, 1}*), and an input value x ∈ X (where the domain X is a subset of {0, 1}*) and computes as its output a pair of updated state information σ’∈ Σ and a finite string y ∈ {0, 1}*. For convenience, we assume that the empty string ε is in the set Σ. Simulator S is always an oracle machine having access to some oracle M. Succinctly, we can write (σ’, y) ← SM(1κ, σ, x). S’s goal is to mimic some oracle We introduce a connector C, which is a dummy functionality whose purpose is merely to connect simulator S to an oracle machine D. A connector C is a stateful machine; that is, it has an internal memory that can store current state information σ ∈ Σ. The state σ is initially set to the empty string ε. Connector C works as follows. Upon receiving an oracle query x ∈ X from distinguisher D, connector C forwards (σ, x) to simulator S and lets S compute (σ’, y) ← SM(1κ, σ, x). Connector C receives the output (σ’, y) from S, updates its own state information from σ to σ’, and returns the value y to D. Consider a distinguisher D 3.2 Definition of indifferentiability: local vs. universalThere are two different versions of the indifferentiability notion. The setting for the notion of indifferentiability is as follows. Let D be an adversary. D’s goal is to distinguish between the real world and the ideal world. In either world, D has access to two oracles. In the real world, we define efficient construction F having access to oracle φ to be indifferentiable from oracle Φ as follows. Consider a polynomial-time simulator S having access to oracle Φ and trying to simulate φ. Simulator S has complete knowledge of F. Consider a polynomial-time adversary D that has access to two oracles and is expected to output a bit at the end of each game execution. D has complete knowledge of not only F but also S. The notion of indifferentiability for F (together with S and D) is given by the following two different games: in the real game, D is given access to two oracles F and φ, while in the ideal game, D is given access to two oracles φ and S. We define the advantage
where the probability is taken over the coin tosses φ and Φ. Definition 1 (Local: Maurer et al. [5]). Let F be an efficient construction. We say that F is indifferentiable from the random oracle (in the sense of Maurer et al.’s definition) if for any polynomial-time adversary D there exists an efficient simulator S and a negligible function ε(κ) such that the inequality Definition 2 (Universal: Coron et al. [4]). Let F be an efficient construction. We say that F is indifferentiable from the random oracle (in the sense of Coron et al.’s definition) if there exists an efficient simulator S such that for any polynomial-time adversary D there exists a negligible function ε(κ) satisfying the inequality To avoid confusion, we give specific names to these two notions: we say that an efficient construction F is locally indifferentiable if it is indifferentiable in the former sense and universally indifferentiable if it is indifferentiable in the latter sense. Clearly, universal indifferentiability implies local indifferentiability. Remark 1. It seems that the two definitions arise from the difference in purpose. The main purpose of the former definition is to discuss security under the system compositions, and the definition indeed gives a necessary and sufficient condition for composability. On the other hand, the purpose of the latter is to measure how good a construction is, because the existence of a universal simulator shows that it is indeed a good construction, with the simulator being the inverse construction. Remark 2. We emphasize that adversaries D and simulators S are merely algorithms (Turing ma- chines). Hence, a simulator S is not allowed to observe the queries/replies made in the interaction between D and Φ*3. Moreover, note that D is not allowed to observe the running time of oracles with which it interacts because any oracle interaction takes exactly unit time. 3.3 Definition of MGF functionality/securityTo formalize the functionality of MGFs, we define MGFs and their corresponding random oracle (i.e., ideal MGF function), and we define hash functions and their corresponding random oracle (i.e., ideal hash function). We start by giving a definition of an MGF. Intuitively, an MGF is defined as a concrete function that takes as its input a seed x together with the requested length l and returns a string of l bits. An ideal MGF is simply a monolithic random function having such an interface. Definition 3 (MGF). An MGF is a VIL-VOL function F: {0, 1}* × {1}*→ {0, 1}* satisfying the following two properties: 1. Length: For all x ∈{0, 1}*X and l ∈ Z≥0, we have |F (x, 1l) | = l. 2. Prefix: For all l; l’ ∈ Z≥0 such that l ≤ l’, we have F (x, 1l) = [F (x, 1l’)]l. The MGF random oracle The notion of MGFs corresponds to the original definition of VIL/VOL random oracles by Bellare and Rogaway [6]; an MGF specifies the length of outputs. The notion of MGFs is also compatible with the interface of the MGF1, which has been widely standardized [13], [17]–[19]. Below, we give one of several possible definitions of a hash function. Definition 4 (Hash function). A hash function is a VIL/FOL function H: {0, 1}*→ {0, 1}n, where n ∈ N. The random oracle We say that efficient construction F of an MGF using random oracle φ =
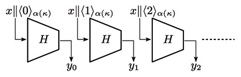
4. Analysis of counter-based MGFsFirst, we define the counter-based MGF F. Then, we show that F cannot be proven to be indifferentiable from 4.1 Description of the counter-based MGFThe counter-based MGF F: {0, 1}* × N → {0, 1}* uses a hash function H: {0, 1}*→ {0, 1}n. Here, the output length n is a polynomial function of the security parameter κ. The description of F is as follows: 1. Receive an input (x; l) ∈{0, 1}*× N. 2. Set t = 3. Compute yi = H(x||⟨i⟩α(κ)) for i = 0, …, t – 1. 4. Output F(x, l) = y0|| ··· ||yt – 2||[yt – 1]r. In the above, ⟨i⟩α(κ) denotes an α(κ)-bit representation of integer i, where α(κ) is a polynomial in κ. The counter-based MGF is illustrated in Fig. 1.
4.2 Proof that the counter-based MGF is locally indifferentiableWe prove that the counter-based MGF M defined above is locally indifferentiable. Intuitively, the proof goes as follows. Given an efficient distinguisher D, there exist polynomials qD(κ) and lD(κ). Using these polynomials, we can construct an efficient simulator S that sets the advantage of D to zero. Theorem 1. The counter-based MGF M is locally indifferentiable from an ideal MGF M. Proof. Let D be an efficient distinguisher attacking the counter-based MGF F. We show that there exists an efficient simulator S that makes the advantage function of D equal to 0. Let qD(κ) and lD(κ) be polynomial functions restricting the capacity of D. Using these polynomials, we construct a simulator SΦ(1κ, σ, x) as follows. 1. Receive an 2. If (X, Y ) is already in state σ, then return (σ, Y ) to adversary D. 3. If X = x||⟨i⟩α(κ) and i · n(κ) ≤ lD(κ), then compute Y = [Φ (x,(i+1) · n(κ))]n(κ) by asking Φ oracle and obtain updated state σ’ by adding (X, Y ) to σ and return (σ’, Y) to adversary D. 4. If X = x||⟨i⟩α(κ) and i · n(κ) > lD(κ), then choose a random string Y ∈U {0, 1}n(κ) and obtain updated state σ’ by adding (X, Y ) to σ and return (σ’, Y ) to adversary D. We see that S is an efficient simulator because we have tS = O(qDlD), qS = qD, and lS = lD + n. We also observe that S perfectly mimics the oracle 4.3 Proof that the counter-based MGF is not universally indifferentiableNow we prove that the counter-based MGF F is not universally indifferentiable from an ideal MGF Φ. Intuitively, we argue that any single simulator S will fail when a distinguisher D starts by raising a query x||⟨i⟩α(κ) for some huge i. In such a case, S is forced to decide whether or not to send a query (x, n(i + 1) to its Φ oracle. If the value i is within the resource bounds of D, then S should certainly send such a query (and return the consistent value). On the other hand, if i is beyond the resource bounds of D, then S should simply ignore making such a query (and return a random string). However, S cannot make such a decision intelligently because it is not allowed to have any information about D. Theorem 2. The counter-based MGF F is not universally indifferentiable from an ideal MGF Φ. Proof. Suppose, on the contrary, that there exists a single simulator S that works against any efficient distinguisher. We show that this leads to a contradiction. Let κ be the security parameter. Throughout the proof, we set the seed x to be a one-bit string “0,” i.e., x = 0. First, we define two types of events, Queryi and Replyi, for i ∈ Z≥0. Every distinguisher that we construct in the current proof sends a query of the form x||⟨i⟩α(κ), for some i ∈ Z≥0, to its H oracle at the beginning of each game execution. Let Queryi denote this event. After the event Queryi, the simulator S is given a pair (ε, x||⟨i⟩α(κ)) (ε being the null state) and is required to return updated state σ’ and a string y ∈ {0, 1}n(κ). Let Replyi denote this event, i.e., the event that (σ’, y) ← SΦ(1κ, ε, x||⟨i⟩α(κ)) is computed and returned to the intermediary I. Next, we define probabilities pi(κ) for i ∈ Z≥0. Let Tunei denote the event, which occurs between Queryi and Replyi, of simulator S sending a query (x, 1l) to its Φ oracle for some l ≥ n(κ) · i + 1. Put pi(κ)= Pr[Tunei]. Since we fix the seed x, the probability pi(κ) is well-defined for each pair of an integer i ∈ Z≥0 and a security parameter κ ∈ N. Note that the probability pi(κ) does not depend on the description of distinguishers and is defined over the coins of S and Φ (S may send some other queries to its Φ oracle in the interval). We define a function j: N→ Z≥0 We show that j cannot be bounded by a polynomial function. Suppose, on the contrary, that there exists some polynomial function f (κ) and an integer N1 ∈ N such that for all security parameters κ > N1 the inequality j(κ) < f (κ) holds. If such a polynomial function f exists, then it implies that there also exists a distinguisher 1. Choose a random index i ∈U {0, 1 ..., f (κ) – 1}, 2. Send a query x||⟨i⟩α(κ) to its S oracle and receive a string y ∈ {0, 1}n(κ), 3. Send a query (x, 1n(κ) · (i + 1)) to its Φ oracle and receive a string y ∈ {0, 1}*, 4. y’ ← [y]n(κ), 5. If y = y’, return 1; otherwise, return 0. Observe that the distinguisher Df makes exactly two queries, each being at most n(κ) · f(κ) bits. Therefore, Df is an efficient distinguisher. We show that this is in direct contradiction to the requirement that the success probability of the distinguisher Df be negligible. To see this, let us compute the advantage Advmgf(Df (1κ)) for sufficiently large security parameters κ > N1. If Df interacts with the pair (F, φn(κ)), we can easily verify that Df outputs 1 with probability 1. On the other hand, if Df interacts with the pair (Φ, S), we claim that the probability of Df (1κ) returning 1 is at most 1 – f(κ)–1 · (2/3 – 2–n(κ)). To see this, let One denote the event 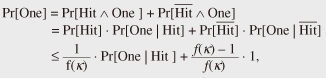
and we also have 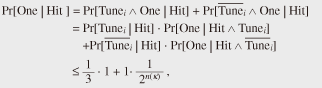
where the variable i denotes the value selected in line 1 of the description of the distinguisher 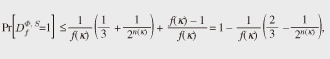
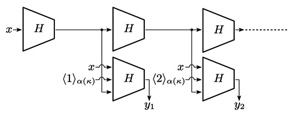
and we also get which is clearly not a negligible function. Thus, we have shown that function j(κ) is not bounded by any polynomial function. We show that this also leads to a contradiction, creating another type of distinguisher. To construct the distinguisher, we first identify a polynomial g(κ) as follows. Consider an initial query x||⟨i⟩α(κ). This leads to an input (1κ, σ, x||⟨i⟩α(κ)) to the simulator S, where σ = ε and x = 0. Hence, the length of such an input is κ + 0 + 1 + α(κ), which is a polynomial in κ. Since the bound lS is a polynomial in the input length, we can regard lS as a polynomial in κ, which we define as g(κ) = lS (κ +1 + α(κ)). Now that we have identified a polynomial function g(κ), we construct the distinguisher 1. i ← min (g(κ) +1, 2α(κ) – 1) 2. Send a query x||⟨i⟩α(κ) to its S oracle and discard whatever is received, 3. Return 1. Next, we find a security parameter κ1 for which running Dg with S leads to a contradiction. Observe that there exists some integer N0 ∈ N such that for all κ > N0, the inequality g(κ) + 1 < 2 α(κ) – 1 holds because the left-hand side is a polynomial in κ whereas the right-hand side is an exponential function of κ. Now recall that j(κ) is not bounded by any polynomial function, which implies that there exists some integer κ1 > N0 such that g(κ1) + 1 <j(κ1). Here, it is important to note that we have Finally, by setting the security parameter κ to κ1, we find a contradiction in the simulator’s bound lS when running Dg. The distinguisher Dg sends its S oracle a query x||⟨g(κ1) + g(κ1) = lS (κ1 + 1 + α(κ1)) ≥ l ≥ n(κ1) · (g(κ1) + 1), which is a contradiction. 5. Analysis of chained MGFsOur results for the counter-based MGF raise the question of whether there exists an MGF construction that can be proven to be universally indifferentiable from an ideal MGF. In this section, we present one such construction: the chained MGF. As an example of the chained MGF, we describe the Double-Pipeline Iteration Mode specified in NIST SP800-108 [20]. We then prove that the Double-Pipeline Iteration Mode is universally indifferentiable from an ideal MGF. 5.1 Description of the Double-Pipeline Iteration ModeThe Double-Pipeline Iteration Mode specified in NIST SP800-108 [20] F: {0, 1}* × N → {0, 1}* uses a hash function H: {0, 1}*→ {0, 1}n. Here, the output length n = n(κ) is a polynomial function of the security parameter κ such that the inequality n(κ) > κ holds for all κ ∈ N. The description of F is as follows: 1. Receive an input (x, l) ∈ {0, 1}* × N. 2. Set t = 3. Compute 4. Output F(x, l) = y1 || ··· ||yt – 1||[yt]r. In the above, ⟨i⟩α(κ) denotes an α(κ)-bit representation of integer i, where α(κ) is a polynomial in κ. The Double-Pipeline Iteration Mode is illustrated in Fig. 2.
Since the resource bound of the Double-Pipeline Iteration Mode F is O(|x|l) and the output length is O(l), the Double-Pipeline Iteration Mode F is efficient. 5.2 Proof that the Double-Pipeline Iteration Mode is universally indifferentiableThe Double-Pipeline Iteration Mode F is indifferentiable from MGF random oracle Theorem 3. The Double-Pipeline Iteration Mode Proof. We construct a simulator S that has access to oracle 1. Receive an 2. If the query X ∈{0, 1}* is stored, return the stored answer to adversary D. 3. If X = x, return a random string υ1 ∈U {0, 1}n to D and store (v0 = x, v1, 1, “chained”). 4. If X = vi and (vi-1, vi, i, “chained”) is stored, return a random string vi+1 ∈U {0, 1}m to D and store (vi, vi+1, i + 1; “chained”). 5. If X= υi ||⟨i⟩α(κ)||x and (vi-1, vi, i; “chained”) is stored, return yi = [ 6. Otherwise, return a random string Y ∈ U {0, 1}n to D and store (X, Y, “junk”). Now we argue that simulator S is a polynomial-time adversary. To see this, let tD, qD, lD be polynomial functions such that D(κ) ∈ D(tD, qD, lD). Since S makes S perfectly simulates oracle However, the Double-Pipeline Iteration Mode outputs n/2n bits per hash function computation, so it is less efficient than a counter-based MGF, which outputs n bits per hash function computation. 6. ConclusionWe have shown that the counter-based MGF cannot be proven to be naturally indifferentiable from the ideal MGF. As a solution to this problem, we have shown that a chained MGF is proven to be indifferentiable from the ideal MGF. However, the chained MGF is less efficient than the counter-based MGF because it outputs fewer bits per invocation and operates in a non-parallelizable manner. It might be worth performing a more detailed study of this security/performance tradeoff because the current work opens up other possibilities for new MGF constructions that are indifferentiable from the ideal MGF and at the same time more efficient (or more secure) than the chained MGF. References
|
|||||||||||||||||||||||||||||||||||||||||||||||||