|
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
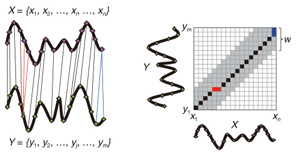
Regular Articles Vol. 11, No. 1, pp. 34–43, Jan. 2013. https://doi.org/10.53829/ntr201301ra1 Subsequence Matching in Data StreamsAbstractSubsequence matching is a basic problem in the field of data stream mining, and dynamic time warping (DTW) is a powerful similarity measure often used for subsequence matching; however, the straightforward method using DTW incurs a high computation cost. In this article, we describe two subsequence matching problems in data streams—(1) the similarity between a query sequence and a data stream and (2) the similarity between data streams—and we present effective algorithms to solve these problems. We also introduce some applications using these algorithms. 1. IntroductionData streams have attracted interest in various fields (theory, databases, data mining, and networking) because of their many important applications including financial analysis, sensor network monitoring, moving object trajectories, web click-stream analysis, and network traffic analysis. Efficient monitoring of time-series data streams is a fundamental requirement for these applications, and subsequence matching is an important technique for this. We consider two problems with subsequence matching over data streams: the similarity between a query sequence and data stream and the similarity between data streams. In the former problem, one is a fixed sequence and the other is an evolving sequence. This approach works well if we have already determined the patterns we want to find. By contrast, the latter problem focuses on co-evolving sequences and reveals hidden patterns between them without preliminary knowledge. Unlike the traditional setting, the sampling rates of streams are often different, and their time period varies in practical situations. Subsequence matching should address asynchronous data and should be robust against noise and provide scaling along the time axis. We focus on dynamic time warping (DTW) as a similarity measure for subsequence matching over data streams. DTW is typically applied to limited situations in an offline manner. Since data streams arrive online at high bit rates and are potentially unbounded in size, the computation time and memory space increase greatly. Ideally, we need a solution that can return correct results without any omissions, even at high speed. This article presents the streaming algorithms SPRING and CrossMatch for subsequence matching. These are one-pass algorithms that are strictly based on DTW and that guarantee correct results without any omissions. We describe the basic ideas behind each algorithm and show how these algorithms work in relation to data stream processing. Moreover, we focus on sensor network monitoring as an application of subsequence matching and discuss the differences between the two algorithms. 2. Background2.1 Related workSimilarity search over time-series data has been studied for many years. Most methods focus on similarity queries for static datasets with a query sequence. Specifically, given a query sequence and a distance threshold, a similarity query finds all the sequences or subsequences that are similar to the query sequence. The basic idea is to transform the sequence into the frequency domain using a discrete Fourier transform (DFT) and then to extract the few features from the resultant frequency-domain sequence [1]. Euclidean distance is used as a similarity measure. Other feature extraction functions include discrete wavelet transform (DWT) [2], singular value decomposition (SVD) [3], piecewise aggregate approximation (PAA) [4], and adaptive piecewise constant approximation (APCA) [5]. These functions have been proposed to reduce the number of dimensions of the time-series. Since the Euclidean distance treats sequence elements independently, it cannot be used to calculate the distance between sequences whose lengths are different. DTW has been adopted to overcome these problems [6]; it is a widely used similarity measure that allows time-axis scaling. The DTW distance can be computed using dynamic programming techniques. Therefore, DTW is typically a much costlier approach than the Euclidean distance. To address the cost issue, several methods have been proposed that use a lower bound to refine the results and envelope techniques to constrain the computation cells [7]¡Ý[10]. Similarity search over data streams has recently attracted more research interest. In contrast to a setting where the data sequences are fixed, data streams arrive irregularly and are frequently updated. Therefore, incremental computation techniques that use the previous feature when computing the new feature are required. Several discriminative methods have been proposed for subsequence matching with a query sequence. These include subsequence matching based on prediction [11], approximate subsequence matching with data segmentation and piecewise line representation [12], subsequence matching supporting shifting and scaling in the time and amplitude domains [13], and subsequence matching based on DTW with batch filtering [14]. Another important area is pattern discovery between data streams. Mueen et al. [15] presented the first online motif discovery algorithm to accurately monitor and maintain motifs, which represent repeated subsequences in time-series, in real time. Papadimitriou et al. [16] proposed an algorithm for discovering optimal local patterns, which concisely describe the main trends in data streams. In summary, there have been many previous studies on similarity search over data streams; however, none of them have addressed effective subsequence matching based on DTW. We formally define two problems for subsequence matching and present efficient and effective algorithms to solve them. 2.2 DTWDTW is a transformation that allows sequences to be stretched along the time axis to minimize the distance between them. The DTW distance of two sequences is the sum of the tick-to-tick distances after the two sequences have been optimally warped to match each other. An illustration of DTW is shown in Fig. 1. The left figure is the alignment by DTW for measuring the DTW distance. To align two sequences, we construct a time warping matrix as shown in the right figure (the warping scope w will be described in section 4.1). The warping path is a set of grid cells in the time warping matrix; this set of grid cells represents the optimal alignment between the sequences. Consider two sequences, X = (x1, x2, ..., xn) of length n and Y = (y1, y2, ..., ym) of length m. Their DTW distance D(X, Y ) is defined as
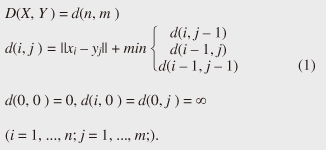
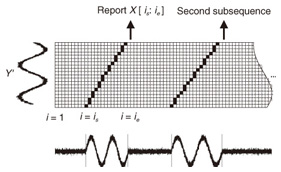
Note that ||xi ¡Ý yj|| = (xi - yj)2 is the distance between two numerical values in cell (i, j) of the time warping matrix. Note that other choices (e.g., absolute difference ||xi ¡Ý yj|| = |xi - yj|) can also be used; the algorithms we present in this article are completely independent of the choice made. Specifically, DTW requires O(nm) time because the time warping matrix consists of nm elements. Note that the space complexity is O(m) because the algorithm needs only two columns (i.e., the current and previous columns) of the time warping matrix to compute the DTW distance. In the problem of subsequence matching with a query sequence, given an evolving sequence X = (x1, x2, ..., xn) and a fixed-length query sequence Y = (y1, y2, ..., ym), we want to find the subsequences of X that are similar to Y in the sense of the DTW distance. By contrast, in the problem of subsequence matching between data streams, given two evolving sequences X = (x1, x2, ..., xn) and Y = (y1, y2, ..., ym), we want to find the subsequence pairs, namely the common local patterns over data streams. We will give the exact definitions for these problems later (in sections 3.1 and 4.1). In both settings, naïve ways of subsequence matching require unfeasible computation time and memory consumption in data stream processing. We show that our approaches offer considerable improvement without loss of accuracy. 3. Subsequence matching with a query sequence3.1 Problem definitionData stream X is a discrete, semi-infinite sequence of numbers x1, x2, ¡Ä, xn, ¡Ä, where xn is the most recent value. Note that n increases with every new time-tick. Let X [is : ie] be the subsequence of X that starts from time-tick is and ends at ie. The subsequence matching problem is to find the subsequence X [is : ie] that is highly similar to a fixed-length query sequence Y (i.e., the subsequence with a small value of D(X [is : ie], Y). However, a subtle point should be noted: whenever the query Y matches a subsequence of X (e.g., X [is : ie]), we expect that there will be several other matches with subsequences that heavily overlap the local minimum best match. Overlaps provide the user with redundant information and would slow down the algorithm since all useless solutions are tracked and reported. In our solution, we discard all these extra matches. Specifically, the problem we want to solve is as follows: Problem 1 Given a stream X (that is, an evolving data sequence, which at the time of interest has length n), a query sequence Y of fixed-length m, and a distance threshold e, report all subsequences X [is : ie] such that 1. the subsequences are close enough to the query sequence: D(X [is : ie], Y) ≤ ε, and 2. among several overlapping matches, report only the local minimum; that is, D(X [is : ie], Y) is the smallest value from the set of overlapping subsequences that satisfy the first condition. Hereafter we use the term optimal subsequences to refer to subsequences that satisfy both conditions. 3.2 SPRINGThe most straightforward (and slowest) solution to this problem is to consider all possible subsequences X [is : ie] (1 ≤ is ≤ ie ≤ n) and apply the standard DTW dynamic programming algorithm, which requires O(n2) matrices. The time complexity would be O(n3m) (or O(n2m) per time-tick). This method is extremely expensive. Moreover, it cannot be extended to the streaming case. To solve the problem, we therefore proposed SPRING [17], which is an efficient algorithm. SPRING uses only a single matrix and detects optimal subsequences in stream processing. 3.2.1 Basic ideasOur solution to the problem is based on two ideas. The first idea is star-padding, in which sequence Y is prefixed with a special value ("*") that always gives zero distance. This value stands for the don't care interval, that is, the interval (¡Ý¡ç : +¡ç). Definition 1 (Star-padding) Given a query sequence Y, star-padding of Y is defined as follows. 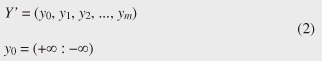 We use Y' to compute the DTW distances of Y and subsequences of X, instead of operating on the original sequence of Y. Given a sequence Y = (y1, y2, ..., ym), we have the star-padding of Y. Let X be a sequence of length n. We can then derive the minimum distance D(X [is : ie], Y) from the matrix of X and Y'. 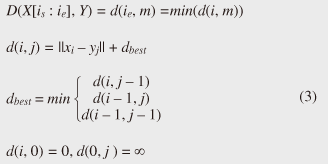 Star-padding dramatically reduces both time and space since we need to update only O(m) numbers per time-tick to derive the minimum distance. Star-padding is a good first step, and it can tell us (a) where the subsequence match ends and (b) what the resulting distance is. However, such applications often also need the starting time-tick of the match. Our second idea is to use a subsequence time warping matrix (STWM): we augment the time warping matrix and record the starting position of each candidate subsequence. Definition 2 (STWM) The STWM contains the value d(i, j), which is the best distance to match the prefix of length i from X with the prefix of length j from Y, and the starting position s(i, j) corresponding to d(i, j). The starting position is computed as 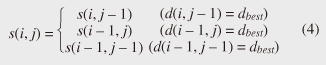 We obtain the starting position of D(X [is : ie], Y) as We update the starting position accompanied by the distance value as well as the distance value itself. By using the matrix, we can identify which subsequence gave the minimum distance during stream processing. 3.2.2 AlgorithmThe way SPRING detects optimal subsequences is shown in Fig. 2. SPRING is carefully designed to (a) guarantee no false dismissals for the second condition of Problem 1 and (b) report each match as early as possible (detailed proofs are given in [17]). For each incoming data point xn, we first incrementally update the m distance values d(n, j) and determine the m starting positions s(n, j). The algorithm reports the subsequence after confirming that the current optimal subsequence cannot be replaced by the upcoming subsequences. That is, we report the subsequence that gives the minimum distance dmin when the d(n, j) and s(n, j) arrays satisfy which means that the captured optimal subsequence cannot be replaced by the upcoming subsequences. Otherwise, the upcoming candidate subsequences would not overlap the captured optimal subsequence. We initialize dmin and the d(n, j) arrays after the output.
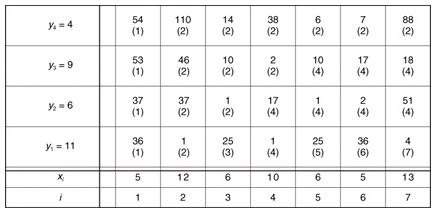
Example 1 Assume that ε = 15, X = (5, 12, 6, 10, 6, 5, 13), and Y = (11, 6, 9, 4) in Fig. 3. The cell (i, j) of the matrix contains d(i, j) and s(i, j). At i = 3, we found candidate subsequence X[2 : 3] whose distance d(3, 4) = 14 below ε. At i = 4, although the distance d(4, 4) = 38 is larger than ε, we do not report X [2 : 3] since d(4, 3) = 2, which means X [2 : 3] can be replaced by the upcoming subsequences. We then capture the optimal subsequence X [2 : 5] at i = 5. X [2 : 5] is reported at i = 7 since we now know that none of the upcoming subsequences will be the optimal subsequence. Finally, because subsequences starting from i = 7 may be candidates for the next group, we do not initialize d(7, 1).
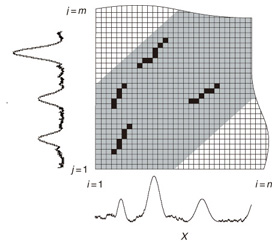
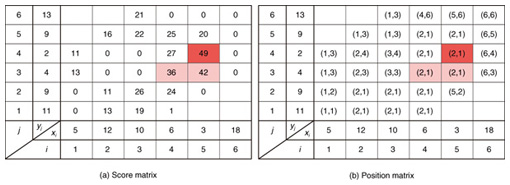
4. Subsequence matching between data streams4.1 Problem definitionWe have focused on finding subsequences similar to a query sequence. In this section, we address subsequence matching between data streams. That is, both sequences X and Y are co-evolving data streams, and we want to identify common local patterns between them. Like data stream X, data stream Y is a discrete, semi-infinite sequence of numbers y1, y2, ¡Ä, ym, ¡Ä, where ym is the most recent value. Note that m increases with every new time-tick. Let Y [js : je] be the subsequence of Y that starts from time-tick js and ends at je. The lengths of X [is : ie] and Y [js : je] are lx = ie ¡Ý is + 1 and ly = je ¡Ý js + 1, respectively. The goal is to find the common local patterns of sequences by data stream processing based on DTW. That is, we want to detect subsequence pairs that satisfy D(X [is : ie],Y [js : je]) ≤ εL(lx, ly), (7) where L is a function that sets the length of the subsequence. The DTW distance increases as the subsequence length increases since it is the sum of the distances between elements. Therefore, unlike the problem where sequence Y is fixed, the distance threshold should be proportional to the subsequence length to detect the subsequence pairs without depending on the subsequence length. Accordingly, we set the distance threshold at εL(lx, ly). In this article, the algorithm uses L(lx, ly) = (lx+ ly)/2, which is the average length of the two subsequences, but the user can make any other choice (e.g., L(lx, ly) = max(lx, ly) or L(lx, ly) = min(lx, ly)). Equation (7) allows us to detect subsequence pairs without regard to the subsequence length. In practice, however, we might detect shorter and meaningless matching pairs owing to the influence of noise. We introduce the concept of subsequence match length to enable us to discard such meaningless pairs. We formally define the cross-similarity between X and Y, which indicates common local patterns. Definition 3 (Cross-similarity) Given two sequences X and Y, a distance threshold ε, and a threshold of subsequence length lmin, X [is : ie] and Y [js : je] have the property of cross-similarity if this sequence pair satisfies the condition D(X [is : ie],Y [js : je]) ≤ ε (L(lx, ly)¡Ý lmin). (8) The minimum length lmin of subsequence matches should be given by the users. The subsequences that satisfy this equation are guaranteed to have lengths exceeding lmin. In addition to subsequence matching with a query sequence, we need to consider several other matches that strongly overlap the local minimum best match. Specifically, in this setting, an overlap is simply where two subsequence pairs have a common alignment, which is defined as follows: Definition 4 (Overlap) Given two warping paths for subsequence pairs of X and Y, their overlap is defined as the condition where the paths share at least one element. Our solution for subsequence matching between data streams is to detect the local best subsequences from the set of overlapping subsequences. Thus, our goal is to find the best match of cross-similarity. Problem 2 Given two sequences X and Y, thresholds ε, and lmin, report all subsequence pairs X [is : ie] and Y [js : je] that satisfy the following conditions. 1. X [is : ie] and Y [js : je] have the property of cross-similarity. 2. D(X [is : ie], Y [js : je])¡Ýε (L(lx, ly)¡Ý lmin) is the minimum value among the set of overlapping subsequence pairs that satisfies the first condition. Hereafter we use the term qualifying subsequence pairs to refer to pairs that satisfy the first condition, and we use optimal subsequence pairs to refer to pairs that satisfy both conditions. Typically, new elements in data streams are usually more significant than those in the distant past. To limit the number of cells in the matrix and focus on recent elements, we utilize a global constraint for DTW, namely the Sakoe-Chiba band [18] that restricts the warping path to the |i ¡Ý j| ≤ w range (i.e., the gray cells in Fig. 1), where w is called the warping scope. In data stream processing, we compute the cells from a recent element to an earlier element of the warping scope w. If m = n, the warping scope is exactly equal to the Sakoe-Chiba band. 4.2 CrossMatchTo solve the problem of cross-similarity, the most straightforward solution is to consider all possible subsequences of X [is : ie] (1 ≤ is < ie ≤ n), and all possible subsequences of Y [js : je] (1 ≤ js < je ≤ m) in the warping scope and apply the standard DTW dynamic programming algorithm. Let w be the warping scope (the gray cells in the figure). The solution requires O(nw2+mw2) time (per update) and space because it has to handle a total of O(nw+mw) matrices to compute the DTW distance. If we prune dissimilar subsequence pairs and reduce the number of matrices, the distance computations become much more efficient. Our method, CrossMatch [19], finds good matches in a single matrix efficiently by pruning the subse-quences (see Fig. 4).
4.2.1 Basic ideasTo identify the dissimilar subsequences early, we propose computing the DTW distance indirectly by using a scoring function. The scoring function computes the maximum cumulative score corresponding to the DTW distance with a score matrix. The score is determined by accumulating the difference between the threshold and the distance between the elements in the score matrix. Thus, we can recognize a dissimilar subsequence pair since the score has a negative value if the subsequence pair does not satisfy the first condition of Problem 2. The scoring function initializes the negative score to zero and then restarts the computation from the cell. This operation allows us to discard unqualifying, non-optimal subsequence pairs. Definition 5 (Score matrix) Given two sequences, X = (x1, x2, ..., xn) and Y = (y1, y2, ..., ym), and the warping scope w, score V(X [is : ie], Y [js : je]) of X [is : ie] and Y [js : je] defined as follows: 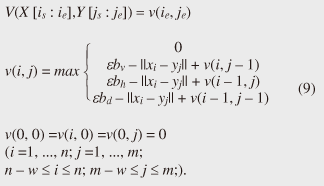 Symbols bv, bh, and bd in Eq. (9) indicate a weight function for each direction, which makes transformation between the score and the DTW distance possible. These values are determined as subsequence length L. For example, for L(lx, ly) = (lx+ly)/2, we obtain bv = bh =1/2 and bd =1, respectively. The scoring function is designed so that the sum of the weights on the warping path is equal to subsequence length L. Therefore, it guarantees transformation between the DTW distance and the score, and it finds the qualifying subsequence pairs without any omissions (detailed proofs are given in [19]). The DTW distance of a subsequence pair is computed from the score and the subsequence length as 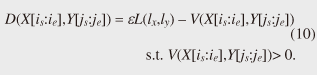 Equation (10) holds for the time warping and the score matrices, which have the same starting position (is, je). The scoring function tells us the subsequence match ends and the subsequence score. However, we lose the information about the starting position of the subsequence. This is the motivation behind our second idea, a position matrix: we store the starting position to keep track of qualifying subsequence pairs in a streaming fashion. Definition 6 (Position matrix) The position matrix stores the starting position of each subsequence pair. The starting position p(i, j) corresponding to score v(i, j) is computed as: 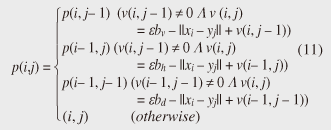 The starting position is described as a coordinate value; p(ie, je) indicates the starting position (is, js) of the subsequence pair X [is : ie] and Y [js : je]. We can identify the optimal subsequence that gives the maximum score during stream processing by using the score and position matrices. Moreover, the starting position of the shared cell is maintained through the subsequent alignments because we repeat the operation, which maintains the starting position of the selected previous cell. Thus, we know the overlapping subsequence pairs from the fact that the starting positions match. 4.2.2 AlgorithmWe now have all the pieces needed to answer the question: how do we find the optimal subsequence pairs? Every time xn or ym is received at time-tick n or m, our CrossMatch algorithm incrementally updates the score and starting position and retains the end position. We use a candidate array to find the optimal subsequence pair, and we store the best pair in a set of overlapping subsequence pairs. CrossMatch reports the optimal subsequence pair after confirming that it cannot be replaced by the upcoming subsequence pairs. The upcoming candidate subsequence pairs do not overlap the captured optimal subsequence pair if the starting positions in the position matrix satisfy the condition: CrossMatch requires only O(w) (i.e., constant) time (per update) and space. This is a great reduction because the straightforward solution requires O(nw2+mw2) time (per update) and space. Example 2 Assume that we have two sequences X = (5, 12, 6, 10, 3, 18) and Y = (11, 9, 4, 2, 9, 13) as well as ε = 14, lmin = 2, and w = 3 in Fig. 5. To simplify our example with no loss of generality, we assume that xi and yj arrive alternately. At each time-tick, the algorithm updates the scores and the starting positions. At i = 4, we update the cells from (4, 1) to (4, 3) and identify a candidate subsequence, X[2 : 4] and Y[1 : 3], starting at (2, 1), whose score v(4, 3) = 36 is greater than εlmin. At j = 4, we update the cells from (1, 4) to (4, 4). Although we detect no subsequences satisfying the condition, we do not report the subsequence X[2 : 4] & Y[1 : 3] since this pair might be replaced by upcoming subsequences. We then capture the optimal subsequence pair X[2 : 5] & Y[1 : 4] at i = 5. Finally, we report the subsequence as the optimal subsequence at j = 6 since we can confirm that none of the upcoming subsequences can be optimal.
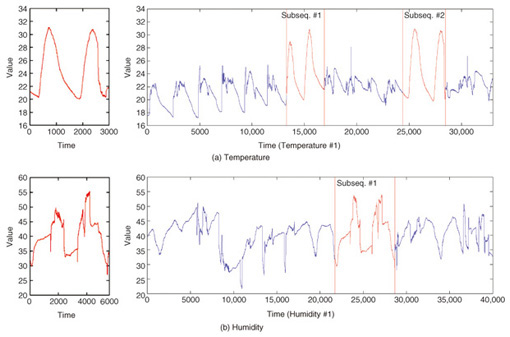
5. Applications of SPRING and CrossMatchOne example of subsequence matching application is sensor network monitoring. In sensor networks, sensors send their readings frequently. Each sensor produces a stream of data, and these streams need to be monitored and combined to detect changes in the environment that may be of interest to users. Users are likely to be interested in one or more sensors within a particular spatial region. These interests are expressed as trends and similar patterns. The optimal subsequences that SPRING detected in temperature and humidity datasets are shown in Fig. 6. The problem that SPRING solves is very simple. Users assign the pattern for which they wish to search. The detected subsequences may be normal patterns, abnormal patterns, frequent patterns, or trends depending on the query sequences.
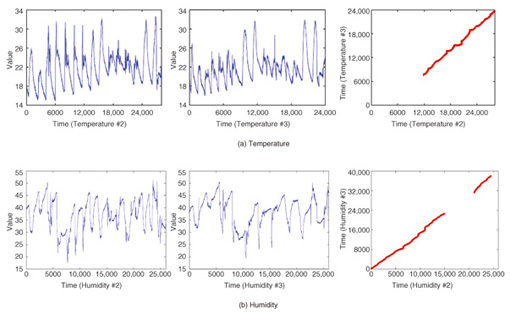
By contrast, CrossMatch focuses on the commonality between data sequences and reveals hidden local patterns. The left graphs in Fig. 7 show similar subsequence pairs in each dataset (i.e., the left and center graphs) as the optimal warping paths. These pairs can be frequent patterns or trends and may be query sequences that users want to search for in the future. This focuses on the similarities of datasets. If we look at the dissimilarities, we can see different applications. For example, the result in Fig. 7(b) can be interpreted as showing that two sensors behaving in the same way have dissimilar intervals. In this case, we can assume a sensor failure and an anomaly in the environment.
6. ConclusionIn this article, we summarized subsequence matching and presented two one-pass algorithms, SPRING and CrossMatch, for subsequence matching over data streams. Both algorithms process at high-speed, exhibit constant time and space consumption, and guarantee correct results. Subsequence matching is applied in several domains, and DTW is a powerful similarity measure for subsequence matching. We believe that our algorithms will contribute to the development of many different intelligent applications. References
|
|||||||||||||||||||||||||||||||||||||||