|
|||||||||
|
|
|||||||||
|
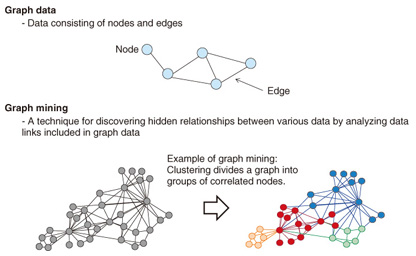
Regular Articles Vol. 11, No. 12, pp. 34–38, Dec. 2013. https://doi.org/10.53829/ntr201312ra1 Efficient Mining Algorithms for Large-scale GraphsAbstractThis article describes efficient graph mining algorithms designed for analyzing large-scale graph data such as social graphs. Graph mining is a technique to analyze the structure of graphs consisting of nodes and edges. We have developed efficient algorithms for two mining tasks: clustering and computing personalized PageRank, for large-scale graphs. Keywords: graph mining, clustering, personalized PageRank 1. IntroductionOne of the methods used to analyze big data is to handle it as graph data. Graph data consist of nodes and edges, where each edge connects two nodes (Fig. 1). Graph mining is a technique for discovering hidden relationships between various data by analyzing graph data. The amount of research on graph data has been increasing rapidly in recent years, and more services that generate graph data, for example, social networking services (SNSs) are being offered. Consequently, graph mining is becoming a major trend in big data analysis. However, efficient techniques for analyzing web-scale graph data have not been well established yet.
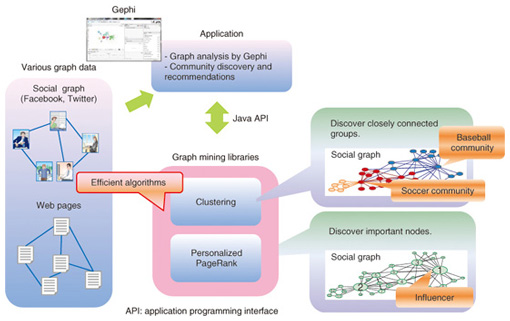
We have been conducting research to design efficient algorithms for graph mining. In February 2013, we announced that we had developed the world’s fastest algorithms for performing two techniques [1]. One is clustering, which involves grouping graph data by taking the density of edges between nodes into account. The other is computing personalized PageRank, which involves searching graph data for nodes with high importance values. These new algorithms make it possible to analyze graph data significantly faster than conventional algorithms. For example, in clustering, conventional algorithms take 4–6 hours to analyze the SNS friendship relationship of 100 million persons. The response time is reduced to only 3 minutes by applying our new algorithm. This substantial reduction results in qualitative changes in analysis, and it provides many applications that bring opportunities for graph mining analysis. We also confirmed that in addition to its high efficiency, our method for clustering (see section 2) achieves a level of accuracy as high as that of the most accurate conventional method (for example, the Louvain method [2]). Conventional algorithms have been devised to speed up the response time at the expense of analysis accuracy. In contrast, our methods have achieved speed-up without loss of accuracy. We have developed both Java libraries and Gephi plug-ins for the algorithms in order to make them widely available. Gephi is a graph analysis and visualization tool that is freely available; it is implemented in Java (Fig. 2).
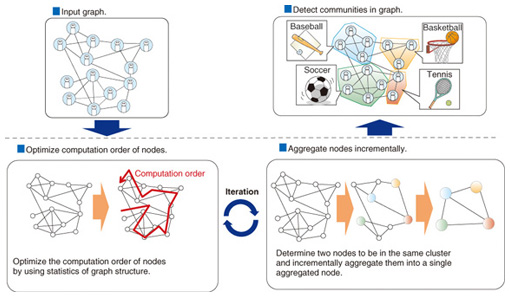
2. Clustering algorithmThe efficiency of our clustering algorithm [3] is achieved by applying two approaches, as illustrated in Fig. 3.
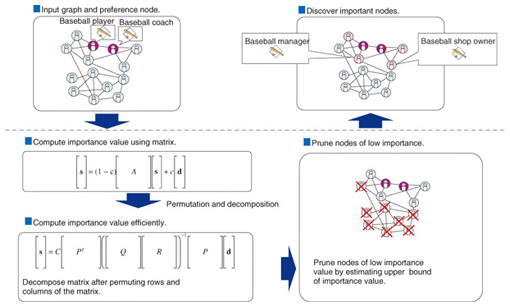
The first approach is to optimize the computation order of nodes during clustering by using the statistics of the graph structure. The degree of a node is defined as the number of edges coming from the node. The computation starts from the node with the smallest degree. This design is based on the bottom-up clustering procedure in which two nodes connected by edges are merged step-by-step until the cluster quality of the graph no longer increases. The merge cost depends on the degree of the nodes; the higher the node degree, the more edges have to be referenced during merging. Consequently, the cost increases. The second approach is to incrementally aggregate two nodes that have been determined to be in the same cluster (or group) into a single aggregated node. This node aggregation is repeated until the cluster quality no longer increases. Since the number of nodes and edges is increasingly reduced through the repeated aggregation, it dramatically improves the response time of clustering. In addition, we introduce an incremental pruning technique for more efficient clustering. That is, if there is a node with only one edge, this node can be aggregated to the cluster of the single neighbor node without computing the increase in the cluster quality. General graph data have many such nodes, so this incremental pruning technique is very effective. The use of these approaches means that our clustering algorithm performs from 10 to 60 times faster than previous algorithms. 3. Personalized PageRank algorithmWe developed an efficient personalized PageRank [4] algorithm for top-k search (Fig. 4) by applying two approaches.
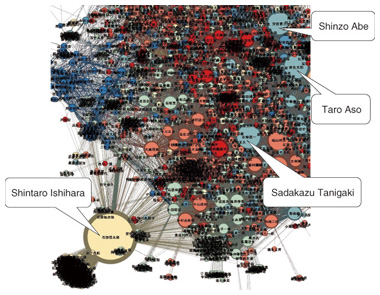
The first approach is to efficiently compute the importance values, that is, the personalized PageRank (PPR) scores of nodes, by permuting rows and columns of the adjacent matrix of input graph data so as to increase the number of zero elements in the matrices, which are obtained by decomposing the adjacent matrix. Since any elements multiplied by zero become zero in the decomposed matrices, we can reduce the computation cost by increasing the number of zero elements. The second approach is that instead of computing the exact PPR scores of all nodes, we efficiently identify top-k nodes with the highest PPR scores by estimating the upper bound of the PPR scores of nodes. The process of identifying top-k nodes is as follows. First, we estimate the upper bound of PPR scores of top-k candidate nodes. Next, we compute the precise PPR scores of the top-k candidate nodes. Then, we continue estimating the upper bound of PPR scores of other promising nodes. We can stop the estimation when the upper bound PPR scores of the promising nodes are lower than the PPR score of the current top-kth node. This means that it is not necessary to compute the precise PPR scores of all nodes in general, which reduces the total cost of PPR computation. As a result, our personalized PageRank algorithm for top-k search is more than 50 times faster than conventional algorithms. 4. Example of graph mining applicationA practical application of our graph mining algorithms is illustrated in Fig. 5. We obtained a social graph of the members of Japan’s House of Representatives and their friends using Wikipedia. Then we applied our algorithms to the graph and analyzed the communities (clusters) of the members and their importance values (PPR scores). The politicians who belong to the same community have the same color in the figure, and those whose importance value is higher have a larger node. There were about 3,000 nodes in total.
We can see in the figure that the size of the Shintaro Ishihara node is the largest. This suggests that he is a very influential person. Meanwhile, the nodes for Shinzo Abe, Taro Aso, and Sadakazu Tanigaki have the same color. This suggests that they belong to the same community. In fact, they all belong to the Liberal Democratic Party. 5. SummaryWe have developed the world’s fastest algorithms for the graph mining tasks of clustering and computing personalized PageRank. We have also implemented both Java libraries and Gephi plug-ins for our algorithms to make the algorithms widely available. We implemented some approaches to make our algorithms highly efficient and successfully applied our algorithms to a social graph extracted from Wikipedia. References
|
|||||||||