|
|||||||||||||||
|
|
|||||||||||||||
|
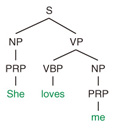
Regular Articles Vol. 12, No. 1, pp. 53–57, Jan. 2014. https://doi.org/10.53829/ntr201401ra1 Statistical Grammar Induction for Natural Language ParsingAbstractParsing, or syntactic analysis, is a fundamental problem in natural language processing. A natural language parser begins with words of input and builds up a syntactic tree, applying grammar rules acquired from language corpora beforehand. This article focuses primarily on the acquisition of grammar rules from language corpora, which is called grammar induction, and describes recent advances in statistical grammar induction for statistical parsing. Keywords: natural language processing, parsing, grammar induction 1. IntroductionParsing, or syntactic analysis, is a fundamental problem in the field of natural language processing (NLP). The resulting analyses are useful for developing high-quality NLP applications such as machine translation, automatic summarization, and information extraction. Consider the English-Japanese translation as an example. English follows the S-V-O word order; that is, the subject comes first, the verb second, and the object third. By contrast, Japanese follows the S-O-V word order. Thus, when translating from one language to another, syntactic information such as subject, verb, and object is necessary for correct word reordering. It is known that the syntactic information of a sentence can be encoded in tree-structured forms such as phrase structure trees and dependency structure trees. Many human-annotated corpora of syntax trees such as Penn Treebank [1] have been developed. An example of a syntax tree is shown in Fig. 1. The tree contains the syntactic categories PRP, NP, VBP, VP, and S, which respectively indicate pronoun, noun phrase, verb, verb phrase, and sentence. A natural language parser begins with words of input, for example, She loves me, and builds up the syntactic tree as shown in Fig. 1, applying grammar rules such as S → NP, VP and VP → VBP, NP.
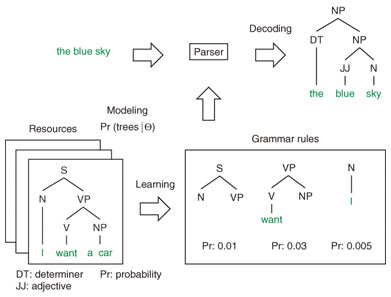
Statistical parsing essentially involves three steps: modeling, learning, and decoding. An illustration of these steps used in building a statistical parser is shown in Fig. 2. Modeling syntax trees is formalized as a probabilistic grammar. Probabilistic grammars consist of a set of structural rules (tree fragments) that govern the composition of sentences, clauses, phrases, and words. Each rule, called an elementary tree, is assigned a probability.
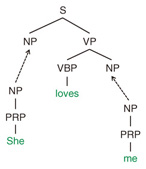
With a probabilistic grammar and a collection of syntax trees, the learning process finds the optimal parameters that fit the training data based on some criteria such as maximum-likelihood estimation. For decoding, the statistical parser searches over a space of all candidate syntactic analyses according to the grammar rules. It then computes each candidate’s probability and determines the most probable parse tree. Some well-known probabilistic grammars for modeling syntax trees, which underlie the state-of-the-art statistical parsers, are reviewed in this article. Additionally, grammar induction algorithms for learning grammar rules based on the probabilistic grammars are introduced. 2. Probabilistic grammarsThis section briefly reviews probabilistic tree substitution grammars (TSGs) and probabilistic symbol-refined tree substitution grammars (SR-TSGs) for statistical modeling of syntax trees. 2.1 TSGsFormally, a TSG is defined by a 4-tuple: G = (T, N, S, R) where - N is a finite set of nonterminal symbols, - T is a finite set of terminal symbols, - S ∈ N is the distinguished start symbol, and - R is a finite set of productions (a.k.a. (also known as) rules). The productions take the form of elementary trees, that is, tree fragments of height ≥ 1. The root and internal nodes of the elementary trees are labeled with nonterminal symbols, and leaf nodes are labeled with either terminal or nonterminal symbols. Nonterminal leaves are referred to as frontier nonterminals and form the substitution sites to be combined with other elementary trees. A derivation is a process of forming a parse tree. It starts with a root symbol and rewrites (substitutes) nonterminal symbols with elementary trees until there are no remaining frontier nonterminals. An example of TSG derivation is shown in Fig. 3. Different derivations may produce the same parse tree. Therefore, recent studies on TSG induction [2], [3] have employed a probabilistic model of TSG and have predicted derivations from observed parse trees in an unsupervised way.
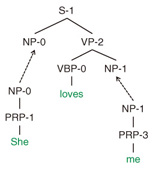
A probabilistic TSG assigns a probability to each rule in the grammar. The probability of a derivation is simply defined as the product of the probabilities of its component elementary trees as follows: where {e} = (e1, e2, …) is a sequence of elementary trees used for the derivation, X = root(e) is the root symbol of e, and p(e|X) is the probability of generating e given its root symbol X. It should be noted that probabilistic TSG assumes a sort of context-free grammars, which means that e is generated conditionally independent of all others given X. Since the derivation of a syntax tree is usually unobserved, our grammar induction task turns out to be inferring the most probable TSG derivation for each syntax tree in an unsupervised fashion. The extracted TSG rules and their probabilities are used to parse raw sentences. 2.2 SR-TSGsThe symbol-refined tree substitution grammar (SR-TSG) proposed previously [4] is an extension of the TSG model where every symbol of the elementary trees can be refined (subcategorized) to fit the training data. An example of SR-TSG derivation is shown in Fig. 4. In the figure, syntactic categories such as S-1 and NP-0 are refined in order to model syntax trees more accurately. For example, grammar rules are likely to generate pronouns such as I and you as subject noun phrases, while generating other objects such as pen and box as object noun phrases. We expect symbol refinement to automatically cluster subject noun phrases as NP-0 and object noun phrases as NP-1. For SR-TSG, it is necessary to infer both TSG derivation and symbol subcategories of every node from a training corpus of syntax trees. In the standard TSG, the extracted SR-TSG rules and their probabilities are used to parse raw sentences.
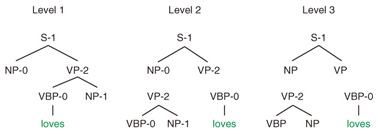
One major issue regarding modeling an SR-TSG is that the space of the grammar rules will be very sparse since SR-TSG allows for arbitrarily large tree fragments and also an arbitrarily large set of symbol subcategories. The authors of the previous study [4] addressed this data sparseness problem by employing a three-level hierarchy to encode a backoff scheme from a set of complex SR-TSG rules to a set of simpler grammar rules. An illustration of a three-level hierarchy for the SR-TSG model is shown in Fig. 5. In the figure, the first level allows every SR-TSG rule. However, the second level only allows tree fragments of height = 1, and the third level only allows tree fragments of height = 1 and unrefined child nodes. To address the data sparseness problem, the probability of the SR-TSG rule (the first level) is interpolated by the probability of simpler tree fragments (second and third levels).
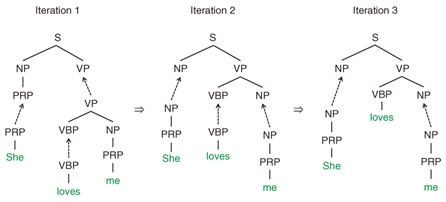
Specifically, the probability distribution of SR-TSG is defined as follows: 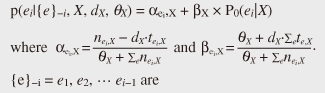 previously generated trees, and nei,X is the number of times ei has been generated in {e}−i. Here, tei,X is the value of an internal variable called table, P0 is called a base distribution over e, and dX and θX are parameters of the model. This probability model is based on the Pitman-Yor process [5]. (See [4] for details.) Roughly speaking, the first term αei‚X is the probability of e based on the number of times the tree fragment has been generated so far. The second term βX × P0 is the smoothing probability of e, which is computed using the simpler grammar rules as shown in Fig. 5. Even if some grammar rule e does not appear in the training corpus, that is, αei,X = 0 the probability of e becomes higher than zero due to the smoothing probability β × P0(e|X). 3. InferenceOnce we define the probabilistic grammar model such as TSG or SR-TSG, we can infer the most probable grammar rules (derivation) from a training corpus of syntax trees. For the inference of grammar rules, Gibbs sampling [6] is one of the most common techniques applied to obtain derivation samples from the posterior distribution. The basic procedure of Gibbs sampling for inferring TSG rules is explained here as an example. The inference of TSG derivation corresponds to inducing substitution nodes. A substitution node is a node of a parse tree that forms the root node of some elementary tree. For example, in Fig. 3, two NP nodes are substitution nodes, while all the other nodes are non-substitution nodes. An illustration of Gibbs sampling for TSG induction is shown in Fig. 6. For each iteration, the Gibbs sampling algorithm works by sampling the value of each binary variable (1 for substitution node and 0 for non-substitution node) according to the posterior distribution in random order. When it reaches convergence, we can obtain the most probable derivation according to the posterior distribution over grammar rules. For the inference of the SR-TSG model, it is necessary to induce substitution nodes plus latent subcategories for every node.
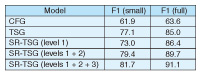
4. Experiment4.1 SettingSome experimental results of statistical parsing using TSG and SR-TSG are introduced in this section. The standard data set for evaluating parsing performance is the Wall Street Journal (WSJ) portion of the English Penn Treebank [1]. The Penn Treebank data set consists of 24 sections; we used sections 2–21 for the training corpus and 23 for testing. For training, the grammar rules are extracted by Gibbs sampling from a collection of syntax trees in the training data. For testing, the algorithm begins with words of input, rather than a syntax tree, and then predicts the syntax tree. The parsing results are obtained with the MAX-RULE-PRODUCT algorithm [7] by using the extracted grammar rules. The accuracy of the predicted syntax trees is evaluated by bracketing the parsing accuracy (F1 score) of the predicted parse trees. 4.2 Results and discussionThe F1 scores of context-free grammar (CFG), TSG, and SR-TSG models [4] are listed in Table 1. The parsing accuracy of the SR-TSG model with three backoff hierarchy settings is also listed in the Table in order to show the effects of backoff smoothing on parsing accuracy. In Table 1, F1 (small) indicates that we used only section 2 (small training data) for training, whereas F1 (full) indicates that we used sections 2–21 (full training data) for training. Moreover, SR-TSG (level 1) denotes that we used only the topmost level of the hierarchy. Similarly, SR-TSG (level 1 + 2) denotes that we used only levels 1 and 2 for backoff smoothing.
The results obtained in the previous study [4] indicate that the best model, SR-TSG (level 1 + 2 + 3), performed the best on both training sets. This suggests that the conventional CFG and TSG models trained naively from the treebank are insufficient to fit the training data due to the context-free assumption and coarse symbol annotations. SR-TSG also assumes context-freeness; however, as we expected, symbol refinement can be helpful with the TSG model for further fitting of the training data and for improving the parsing accuracy. The performance of the SR-TSG parser was strongly affected by its backoff models. SR-TSG (level 1) performed poorly compared with the best model. This result suggests that the SR-TSG rules extracted from the training set are very sparse and cannot cover the space of unknown syntax patterns in the testing set. Therefore, well-designed backoff modeling is essential for the SR-TSG parser. 5. SummaryThis article reported on recent progress in statistical grammar induction for natural language parsing and presented probabilistic TSG and SR-TSG for modeling syntax trees and a Gibbs sampling algorithm for extracting grammar rules. SR-TSG successfully outperformed the TSG model in a standard English parsing task by using a symbol refinement technique and three-level backoff smoothing. References
|
|||||||||||||||