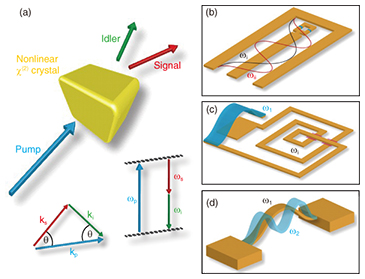
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Regular Articles

Vol. 13, No. 8, pp. 42–52, Aug. 2015. https://doi.org/10.53829/ntr201508ra1

Two-mode Squeezing in an Electromechanical Resonator

Imran Mahboob, Hajime Okamoto, and Hiroshi Yamaguchi

Abstract

A mechanical resonator integrated with piezoelectric transducers enables mechanical nonlinearities to be dynamically engineered to emulate non-degenerate parametric down-conversion. In this configuration, millions of phonons are simultaneously generated in pairs in two macroscopic vibration modes, which results in the amplification of their motion by more than 20 dB. Mechanical two-mode squeezed states are also created in parallel, which exhibit fluctuations 5 dB below the thermal level of their constituent modes and they harbor correlations between the modes that become perfect as their amplification is increased. This remarkable observation of correlations between two massive phonon ensembles establishes the means to create an entangled macroscopic mechanical system at the single phonon level.

Keywords: electromechanical resonator, parametric down-conversion, squeezed-states, phonons

1. Introduction

Electromechanical systems consist of a single degree of mechanical freedom hosting a spectrally pure resonance that is embedded in an electrical transduction circuit, and they have emerged as a versatile platform for a range of technological applications and to study fundamental science [1, 2]. For instance, their small inertial mass and high quality resonance have enabled the development of ultra-precise sensors that can detect a single electron spin and even the mass of a proton leading to a new class of medicinal diagnostic technology [3–5]. The electrical transduction circuit can also enable the underlying potential energy landscape of the mechanical resonator to be dynamically engineered, yielding a range of nonlinear motional dynamics that can be harnessed for both information storage and processing, which brings forth the concept of mechanical computation offering both ultra-low power consumption and the capacity for unprecedented parallel data processing [6–9].

Most tantalizingly, a high frequency mechanical resonator operated at sufficiently low temperatures can even condense into its quantum ground state, where its low mass and spectral purity yield quantum zero point fluctuations that are large enough to be observed, enabling a macroscopic quantum system to be studied [10–12]. In this instance, although the mechanical resonator is composed of billions of atoms, only the phonons sustained by the fundamental resonance mode are quantized, and it corresponds to a tangible vibration of the mechanical element. This phonon picture, namely the collective excitation of atoms in the fundamental vibration mode, enables concepts from atomic molecular optical (AMO) physics developed for photons, that is, a quanta of electromagnetic radiation, to be exploited. Indeed, it is the laser cooling techniques pioneered in AMO physics that have been utilized most successfully to cool the macroscopic mechanical oscillator so that on average, its fundamental mode is occupied by much less than one phonon [13, 14].

Although the notion of a macroscopic mechanical resonator composed of billions of atoms being considered only in terms of the number of phonons sustained by its fundamental mode might seem counterintuitive, this paradigm has successfully been exploited to demonstrate the signature feature of photonics, namely lasing but with the localized phonons in the mechanical resonator [15–18]. Consequently, the ability to cool a solid-state macroscopic mechanical resonator into its ground state opens up the possibility of generating an all-mechanical macroscopic entangled state [10, 19], which would enable foundational aspects of quantum mechanics to be queried such as the nature of the quantum to classical divide and the absence of quantum phenomena in our everyday classical world [20, 21].

2. Two-mode squeezed states

Entangled photons in the guise of two-mode squeezed states were among the first non-classical states of light to be generated in the lab and nowadays are routinely siphoned from spontaneous parametric down-conversion [22]. This typically involves a χ⁽²⁾ nonlinear crystal that is exposed to a strong laser pump beam whose dielectric polarization responds nonlinearly to the pump’s electric field. In this process, a pair of photons—the signal and the idler—are generated at the expense of the pump photons, which conserve both energy and momentum, as depicted in Fig. 1(a). Remarkably, the quantum fluctuations in the amplitude and phase of the generated photon pair are correlated, as encapsulated by the Einstein, Podolsky, and Rosen (EPR) paradox, where their individual fluctuations are amplified, while their relative fluctuations are reduced below the vacuum noise level [23–26]. The EPR paradox recast in the Bell inequality has been routinely violated via the entangled signal and idler photons whose fluctuations remain correlated even when they are separated over distances of kilometers [27, 28]. The non-classical light generated from spontaneous parametric down-conversion has subsequently engendered a whole host of quantum-enabled technologies including quantum communication [29], optical quantum computing [30], quantum teleportation [31], quantum enhanced measurements and metrology [32, 33].

This unprecedented success has led to two-mode squeezed states being translated to other parts of the electromagnetic spectrum, for instance microwaves utilizing superconducting circuits [34]. Specifically, a superconducting resonator terminated with a nonlinear element such as a superconducting quantum interference device (SQUID), as generically depicted in Fig. 1(b), can enable parametric down-conversion [35, 36]. Pumping the SQUID with flux in these so-called Josephson parametric amplifiers (JPAs) yields a nonlinear variation in the boundary conditions of the microwave resonator which creates a frequency modulation in the standing waves it hosts. If the pump frequency coincides with the sum of two modes (say ω_i and ω_ii as depicted in Fig. 1(b)) in the microwave resonator, it non-degenerately amplifies their vacuum noise, generating signal and idler photons in a process reminiscent to that described above where these photons are entangled [37, 38]. Indeed, JPA-like devices have now opened the door to many of the concepts pioneered with optical two-mode squeezed states but in an on-chip microwave circuit that could even be yoked into a quantum computer.

A variation on these microwave circuits has recently emerged in the form of cavity electromechanical systems where the cavity, namely the microwave resonator, is composed of an inductor and capacitor in series, and the mechanical resonator forms a mechanically compliant element of the parallel plate capacitor, thus capacitively coupling the mechanics to the microwaves as generically depicted in Fig. 1(c) [39–41]. Electric fields in the forms of microwaves can be pumped into this hybrid circuit via a capacitively coupled transmission line that nonlinearly modulates the energy stored in the capacitor and hence the frequencies of the mechanics and the cavity. If the pump coincides with the sum frequency of the subsystems (i.e. ω_i and ω₁ as depicted in Fig. 1(c)), it behaves like a non-degenerate parametric amplifier and it creates photons and phonons in pairs that are correlated in a two-mode squeezed state [42, 43]. This remarkable demonstration illustrates that two vastly dissimilar systems, namely light and sound, can be entangled in a macroscopic context, providing a new regime in which quantum physics can be explored [14].

The cavity electromechanical system detailed in Fig. 1(c) straddles the two extremes of light and sound, and it naturally suggests the possibility of a purely mechanical analogue of a two-mode squeezed state in a phonon-cavity electromechanical system as depicted in Fig. 1(d). As in the microwave case, the mechanical resonator can also sustain multiple modes, say ω₁ and ω₂, as shown in Fig. 1(d), which if nonlinearly coupled, could yield non-degenerate parametric amplification. In contrast to the microwave circuit that needs to be engineered with a nonlinear element, namely the SQUID, to enable the modes to couple, the modes in the mechanical resonator can dispersively couple naturally via the strain induced from the motion of a given mode that modifies the restoring potential, that is, the spring constant and hence, the natural frequency of the other modes [44]. Consequently, if the strain in the mechanical element is sinusoidally pumped, it will nonlinearly modulate the frequencies of all the localized modes, and once this modulation coincides with a pair of modes, it will non-degenerately amplify their motion and in the process generate a two-mode squeezed state [45]. Critically, however, an entanglement will only be generated if the constituent modes are initialized in their quantum ground state [10–12], but the ability to harness this interaction, even if the modes in question are thermalized, would lay a pivotal marker on the road to generating an all-mechanical macroscopic entanglement [46].

Fig. 1. (a) Schematic illustration of the spontaneous parametric down-conversion process used to generate non-classical light where the signal and idler photons are entangled in a two-mode squeezed state. This process occurs at the expense of the pump photons where the signal and idler photons conserve both momentum k_p = k_s + k_i, where k is the wavevector, and energy ω_p = ω_s + ω_i. The nonlinear crystals typically used are BBO (beta-barium borate) for Type II down-conversion (where the signal and idler photons have perpendicular polarization) and KDP (potassium dihydrogen phosphate) for type I down-conversion (where the signal and idler photons have parallel polarization). (b) Schematic depiction of a microwave cavity composed from a superconducting metal (orange) and terminated by a SQUID with two Josephson junctions (blue) that can sustain electromagnetic standing waves, for instance ω_i and ω_ii, which are coupled via the SQUID. (c) Cavity electromechanical system with a microwave resonator of frequency ω_i consisting of a spiral inductor and a capacitor and a mechanical resonator of frequency ω₁ which forms a compliable capacitor. Light and sound in these two subsystems are nonlinearly coupled via the oscillating electrical energy stored in the capacitor. (d) Phonon-cavity electromechanical system consisting of two localized mechanical vibration modes ω₁ and ω₂ that are coupled via strain. In all three systems, if the respective flux penetrating the SQUID, the electric field stored in the capacitor, or the mechanical strain are sinusoidally pumped at the sum frequency of their electromagnetic and/or mechanical modes, signal and idler photons and/or phonons are generated that conserve energy but the momentum conservation constraint is relaxed due to their stationary wave nature.

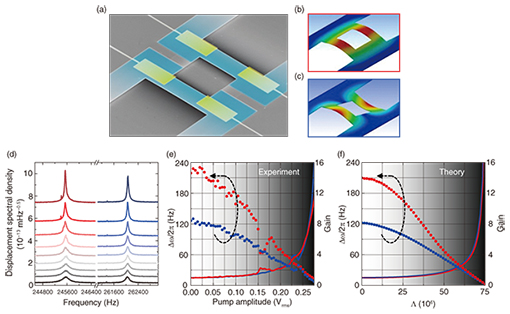
3. Electromechanical resonator

Although degenerate parametric amplification was demonstrated in the early nineties, it could not be used to disentangle correlations between the signal and idler phonons due to their having identical frequencies and being spatially localized to the same mode in the mechanical resonator [47]. Alternatively, a non-degenerate variant of this process in the first two modes of a beam resonator yielded only a modest phonon generation rate, which was insufficient to significantly amplify the thermomechanical fluctuations before they were dissipated, resulting in statistically insignificant correlations [45].

To that end, the electromechanical resonator shown in Fig. 2(a) was developed, which consists of two mechanical elements that are strongly coupled via the exaggerated overhangs between them [48]. This results in the two lowest-order vibration modes shown in Figs. 2(b) and 2(c) that are extracted from a finite element calculation and henceforth labeled symmetric (S) and asymmetric (A), which are closely spaced in frequency. In addition, the spatial profiles of both modes have a large overlap yielding greater strain-mediated dispersive coupling between them. This combination of enhanced dispersive coupling and a smaller frequency separation, almost tending towards a degenerate configuration, is designed to yield larger non-degenerate parametric amplification when the strain in this system is modulated at the sum frequency of both modes.

The piezoelectric effect is utilized in order to modulate the strain in the mechanical modes. By design, the electromechanical system is fabricated from gallium arsenide (GaAs), which is piezoelectrically active [6, 49]. The piezoelectric transducer is formed from a GaAs conducting layer and a gold gate electrode sandwiching an insulating GaAs layer, which is integrated directly into the mechanical element, as shown in Fig. 2(a). Application of an electric field across the transducer generates in-plane strain that can nonlinearly modulate the spring constants and hence, the frequencies of the modes supported by the mechanical system [6].

The Hamiltonian for the electromechanical system in this configuration can then be expressed as:

Here, P and Q are the canonical momentum and conjugate position of the symmetric and asymmetric modes with mass m and natural frequency ω_n, where the summation expresses their kinetic and potential energies. The last term describes the piezoelectrically activated non-degenerate parametric down-conversion with amplitude Λ and frequency ω_p = ω_S + ω_A, that is, at the sum frequency of the modes in question. Ostensibly, this Hamiltonian is classical, which superficially suggests the unavailability of two-mode squeezing. However, the last term is analogous to

(ab + a^†b^†) for non-degenerate parametric down-conversion in cavity electromechanical systems in the frame rotating at the pump frequency, where a, b and a^†, b^† are the annihilation and creation operators for the mechanical and microwave resonators, respectively, and

is the intrinsic coupling rate between them that is enhanced by n pump photons [41–43]. Consequently, Λ encapsulates the intrinsic coupling rate between the symmetric and asymmetric modes that is enhanced by the piezoelectric pump, which results in phonon pairs being simultaneously generated in them [50]. Remarkably, these phonons should still be correlated, even if the two modes are thermalized and far from their quantum ground state, as long as their generation rate exceeds the rate at which they are dissipated from both modes [46].

4. Results

4.1 Non-degenerate parametric amplification

To ascertain if this latter expectation is satisfied, the thermomechanical fluctuations of both modes are spectrally measured via optical interferometry with a 3-µW helium neon laser probing the right element of the electromechanical system at room temperature and in a high vacuum [46]. This measurement reveals the modes with natural frequencies ω_S/ 2π ≈ 246 kHz and ω_A/ 2π ≈ 262 kHz with quality factors Q_n = ω_n/ Δ ω_n of 1300 and 2200, respectively, from their spectral power bandwidth Δ ω_n, and it corresponds to both modes sustaining > 10⁷ phonons. Next non-degenerate parametric down-conversion is activated, and the thermal fluctuations from both modes are monitored. The results of this measurement shown in Fig. 2(d) indicate that as the piezoelectric pump voltage is increased, the thermomechanical fluctuations of both modes are enhanced. This amplification can be referenced to the bare thermal fluctuations, and it yields gains of more than 20 dB that are accompanied by a narrowing of the power spectral bandwidth from both modes, as detailed in Fig. 2(e). At the largest pump amplitudes (>0.275 V_rms) Δ ω_n → 0, resulting in both modes undergoing non-degenerate parametric resonance [51, 52].

To confirm these experimental observations, the equations of motion for both modes are extracted from the Hamiltonian in eq. (1) and reformulated in their rotating frames with Q_n = X_n cos(ω_nt) + Y_n sin(ω_nt), where X_n and Y_n are the slowly varying in-phase and quadrature components. The resultant equations are then numerically solved, as detailed in a previous study [46], and they faithfully reproduce the experimental response as shown in Fig. 2(f), thus verifying that the amplification can be ascribed to non-degenerate parametric down-conversion.

Fig. 2. (a) Scanning electron micrograph of the electromechanical resonator. Each mechanical element is 80 µm long, 20 µm wide, 800 nm thick, and is integrated with two piezoelectric transducers formed from a doped GaAs layer located 300 nm below the surface (blue) and a gold gate electrode (yellow). (b) and (c) The electromechanical resonator sustains symmetric (red) and asymmetric (blue) vibration modes composed from both mechanical elements that are strongly coupled via the two large overhangs between them. (d) Thermomechanical vibrations of both modes when driven by the Langevin force (black) and demodulated in a spectrum analyzer. Activating the non-degenerate parametric down-conversion via the piezoelectric transducers on the left mechanical element from 0 to 0.24 V_rms in 0.03 V_rms increments results in the thermomechanical fluctuations of both modes being amplified. (e) The corresponding amplification gain and spectral power bandwidth (Δω) with pump amplitude increments of 5 mV_rms. (f) This experimental response can be faithfully reproduced by numerically solving the Hamiltonian in eq. (1).

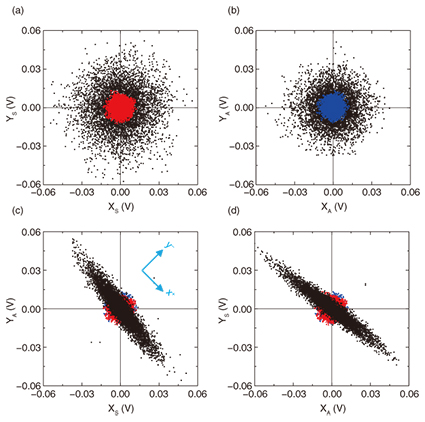
The temporal dynamics of this amplification can also be acquired by mixing the output from the optical interferometer with local oscillators locked onto the resonances of both modes and then demodulated in a phase sensitive detector (PSD). The PSD samples the random displacement fluctuations of the mechanical modes driven by the thermal Langevin force at a rate of 50 ms over a period of 300 s. This yields four time series for the in-phase and quadrature components of both modes, enabling their phase portraits to be constructed as shown in Figs. 3(a) and 3(b). This measurement reveals that the thermal fluctuations of both modes are random and uncorrelated as evidenced by their circular distribution in phase space, indicating all vibration phases are equally likely (red and blue points in Figs. 3(a) and 3(b)). Repeating this measurement with a pump amplitude of 0.25 V_rms confirms that the fluctuations in both modes are enhanced via the non-degenerate parametric down-conversion while retaining their random nature; namely, this amplification is phase insensitive [53].

The observed amplification arises from phonons generated in both modes from the same process; hence, their fluctuations should be correlated. To that end, the cross quadratures are constructed in phase space from the in-phase component of the symmetric mode and the quadrature component of the asymmetric mode and vice versa, as shown in Figs. 3(c) and 3(d). This unveils squeezed distributions where a particular phase orientation is amplified while the perpendicular phase is de-amplified. The narrowness of this distribution implies the existence of correlations between the symmetric and asymmetric modes (if no correlations between the modes existed, the cross-quadratures would yield circular and therefore random distributions) and is the signature feature of a two-mode squeezed state [54, 55]. However, in order to quantitatively verify the existence of correlations between the modes, two criteria need to be satisfied. First, the two-mode squeezed distributions should exhibit smaller fluctuations than the bare distributions; otherwise, the correlations would be washed out by the thermomechanical noise from both modes. Second, the correlations should be statistically evident from the temporal data used to construct the phase portraits.

Fig. 3. (a) and (b) Bare thermal fluctuations of symmetric (red points) and asymmetric (blue points) modes respectively acquired temporally on-resonance and projected in phase space via the in-phase (X) and quadrature (Y) axes. Activating the non-degenerate parametric down-conversion with a pump amplitude of 0.25 V_rms amplifies the fluctuations of both modes while preserving their phase (black points). (c) and (d) The cross quadratures of the pumped measurement X_S: Y_A and X_A: Y_S respectively reconstructed in phase space (black points) reveal two-mode squeezed states have been generated that exhibit fluctuations in a particular phase which are below the bare thermal fluctuations from both modes (red and blue points), while fluctuations in the orthogonal phase are amplified.

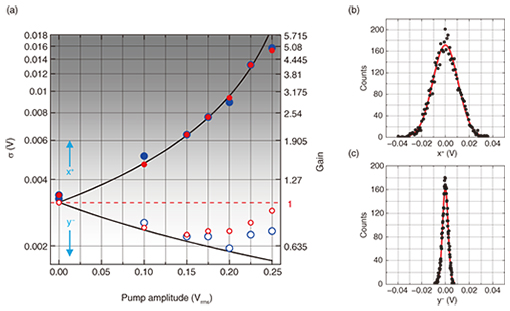
4.2 Squeezing below the thermal noise

The former condition can in fact be visibly confirmed by examining the data in Figs. 3(c) and 3(d), which indicate that the de-amplified phases encompass a narrower distribution than the bare thermal motion from both modes. Quantitatively, new axes x⁺ and y⁻ are introduced, as shown in the inset to Fig. 3(c), onto which the counts in the squeezed distributions are projected, as shown in Figs. 4(b) and 4(c) [46]. This reveals Gaussian profiles with a zero mean displacement, as expected from random fluctuations driven by the thermal Langevin force, whose full width at half maximum can be used to extract their standard deviation σ. This analysis is repeated as a function of non-zero pump amplitude for the cross quadratures X_S: Y_A and X_A: Y_S, where the standard deviations for both the amplified and de-amplified phases corresponding to the x⁺ and y⁻ axes are determined as shown in Fig. 4(a). Naturally, as the pump amplitude is increased, the fluctuations along the x⁺ axis are amplified, while concurrently they are reduced along the y⁻ axis where entropy is conserved in this process. The gain can then be extracted by normalizing with the narrowest standard deviation from the bare thermal distribution (corresponding to the quadrature component of the asymmetric mode). While this slightly overestimates the amplification, it is consistent with the spectral response detailed in Fig. 2(e). However, this normalizing reference underestimates the de-amplification, yielding a conservative 5-dB suppression of the mechanical fluctuations below the thermal level where further reduction is inhibited by noise from the piezotransducers at large pump voltages [46].

Fig. 4. (a) Standard deviation (σ) of the fluctuation distribution from the two-mode squeezed states in phase space when projected onto the rotated axes detailed in Fig. 3(c) as a function of pump amplitude. The amplification along the x⁺ axis is concurrently accompanied with a de-amplification along the y⁻ axis. The red (blue) points correspond to the X_S: Y_A (X_A: Y_S) cross-quadrature reconstruction, and the solid black lines denote the ideal theoretical response extracted from the Hamiltonian in eq. (1). Also shown is the gain normalized to the narrowest bare thermal distribution highlighted by the dashed red line. (b) and (c) The phase portrait from X_A: Y_S with a pump amplitude of 0.2 V_rms projected onto the rotated x⁺ and y⁻ axes reveals Gaussian distributions (points), and the corresponding least squares Gaussian fit (line) enables their standard deviation to be extracted as quantified above.

To confirm these observations, the thermal Langevin force, in the equations of motion extracted from the Hamiltonian in eq. (1), is decomposed into in-phase and quadrature components [16, 45, 46]. This leads to a new set of composite variables for the squeezed distributions given by X_S ± Y_A and X_A ± Y_S that naturally correspond to the rotated axes x⁺ and y⁻ introduced in Fig. 3(c) [37, 46]. The pump-induced gain in the fluctuations of these composite variables can then be extracted from the Langevin correlation function, yielding the solid lines in Fig. 4(a). This verifies that the noise reduction below the thermal level arises from the non-degenerate parametric down-conversion.

4.3 Correlation coefficient

The statistical correlations between the time series for the in-phase and quadrature components from both modes can be analyzed via the absolute correlation coefficient |cov(Z_iZ_i) /σ_Ziσ_Zi|, where Z_i ∈ {X_S, Y_S, X_A, Y_A} and the numerator describes the covariance. Analyzing the bare thermal fluctuations (shown by the red and blue points in Figs. 3(a) and 3(b)) enables a correlation coefficient matrix to be constructed, yielding 16 permutations. However, only 10 combinations are relevant due to their symmetry, as shown in Fig. 5(a). This reveals that the diagonal elements corresponding to the auto-correlations of Z_i yield a coefficient of 1, which indicates that they are perfectly correlated with themselves, as one would expect. However, all the off-diagonal elements yield a coefficient of 0, indicating an absence of correlations; for instance |cov(X_SY_S) /σ_XSσ_YS| ≈ 0, which is unsurprising, as this maps the circular distribution in Fig. 3(a) corresponding to the random uncorrelated fluctuations driven by the thermal Langevin force. Repeating this analysis as a function of pump amplitude ranging from 0.1, 0.2, and 0.25 V_rms as shown in Figs. 5(b)–(d) indicates that the auto-correlations in the diagonal elements remain perfect. However, the off-diagonal elements corresponding to the cross-quadrature phase portraits in Figs. 3(c) and 3(d), namely, X_S: Y_A and X_A: Y_S, emerge and converge towards 1, which implies that the two modes have become perfectly correlated from the simultaneous generation of phonon pairs via non-degenerate parametric down-conversion.

Fig. 5. (a)–(d) Correlation coefficient matrix as a function of pump amplitude from 0, 0.1, 0.2, and 0.25 V_rms, respectively. The diagonal elements (black) correspond to auto-correlations, which naturally yield a coefficient of 1. The off-diagonal elements from X_S: Y_S and X_A: Y_A yield a coefficient of 0, which corresponds to the uncorrelated random fluctuations corresponding to the circular distributions in phase space as shown in Figs. 3(a), 3(b) and are independent of the pump amplitude. In contrast, the off-diagonal elements from the two-mode squeezed states X_S: Y_A (red) and X_A: Y_S (blue) converge towards a coefficient of 1 as the pump amplitude is increased, implying that the two mechanical vibration modes have become perfectly correlated via the simultaneous generation of signal and idler phonons in pairs from the non-degenerate parametric down-conversion.

5. Implications and outlook

Although both mechanical modes sustain more than 10 million phonons at room temperature, the simultaneous generation of phonon pairs from the non-degenerate parametric down-conversion occurs at a rate that renders their fluctuations indistinguishable. Thus, remarkably, these thermalized macroscopic mechanical vibration modes become perfectly entwined in a two-mode squeezed state. Ultimately, if the modes can be operated with phonon populations of much less than one, then these correlations will manifest themselves in a macroscopic all-mechanical entanglement [10, 42, 56]. Access to such a state would be extremely tantalizing, as it would provide an invaluable platform to investigate the absence of quantum mechanical phenomena in our everyday classical world [20].

From a technological point of view, these results herald the emergence of quantum optics to phononics, and thus, concepts such as quantum cryptography and optical quantum computing could potentially be harnessed with sound in a microchip. More immediately, the possibility of even greater squeezing becomes available via more strongly coupled modes in conjunction with a more efficient piezoelectric pump [57]. This enhanced squeezing would not only offer detectors that could operate below the quantum limit, yielding unprecedented sensitivities for metrological applications [33] and fundamental science [58], but it could even be utilized to create room temperature entanglements, thus bringing quantum sound into a more technologically accessible regime [59].

References

[1]	M. L. Roukes, “Nanoelectromechanical Systems Face the Future,” Physics World, Vol. 14, No. 2, pp. 25–31, 2001.
[2]	K. L. Ekinci and M. L. Roukes, “Nanoelectromechanical Systems,” Rev. Sci. Instrum., Vol. 76, No. 6, p. 061101, 2005.
[3]	D. Rugar, R. Budakian, H. J. Mamin, and B. W. Chui, “Single Spin Detection by Magnetic Resonance Force Microscopy,” Nature, Vol. 430, No. 6997, pp. 329–332, 2004.
[4]	J. Chaste, A. Eichler, J. Moser, G. Ceballos, R. Rurali, and A. Bachtold, “A Nanomechanical Mass Sensor with Yoctogram Resolution,” Nature Nanotech., Vol. 7, No. 5, pp. 301–304, 2012.
[5]	J. L. Arlett, E. B. Myers, and M. L. Roukes, “Comparative Advantages of Mechanical Biosensors,” Nature Nanotech., Vol. 6, No. 4, pp. 203–215, 2011.
[6]	I. Mahboob and H. Yamaguchi, “Bit Storage and Bit Flip Operations in an Electromechanical Oscillator,” Nature Nanotech., Vol. 3, No. 5, pp. 275–279, 2008.
[7]	R. L. Badzey and P. Mohanty, “Coherent Signal Amplification in Bistable Nanomechanical Oscillators by Stochastic Resonance,” Nature, Vol. 437, No. 7061, pp. 995–998, 2005.
[8]	I. Mahboob, E. Flurin, K. Nishiguchi, A. Fujiwara, and H. Yamaguchi, “Interconnect-free Parallel Logic Circuits in a Single Mechanical Resonator,” Nature Commun., Vol. 2, p. 198, 2011.
[9]	M. L. Roukes, “Mechanical Computation, Redux?”, IEEE IEDM Technical Digest, pp. 539–542, 2004.
[10]	A. D. O’Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang, M. Weides, J. Wenner, J. M. Martinis, and A. N. Cleland, “Quantum Ground State and Single-phonon Control of a Mechanical Resonator,” Nature, Vol. 464, No. 7289, pp. 697–703, 2010.
[11]	J. D. Teufel, T. Donner, D. Li, J. W. Harlow, M. S. Allman, K. Cicak, A. J. Sirois, J. D. Whittaker, K. W. Lehnert, and R. W. Simmonds, “Sideband Cooling of Micromechanical Motion to the Quantum Ground State,” Nature, Vol. 475, No. 7356, pp. 359–363, 2011.
[12]	J. Chan, T. P. Mayer Alegre, A. H. Safavi-Naeini, J. T. Hill, A. Krause, S. Gröblacher, M. Aspelmeyer, and O. Painter, “Laser Cooling of a Nanomechanical Oscillator into Its Quantum Ground State,” Nature, Vol. 478, No. 7367, pp. 89–92, 2011.
[13]	T. J. Kippenberg and K. J. Vahala, “Cavity Optomechanics: Back-Action at the Mesoscale,” Science, Vol. 321, No. 5893, pp. 1172–1176, 2008.
[14]	M. Aspelmeyer, P. Meystre, and K. Schwab, “Quantum Optomechanics,” Phys. Today, Vol. 65, No. 7, pp. 29–35, 2012.
[15]	I. S. Grudinin, H. Lee, O. Painter, and K. J. Vahala, “Phonon Laser Action in a Tunable Two-level System,” Phys. Rev. Lett., Vol. 104, No. 8, p. 083901, 2010.
[16]	I. Mahboob, K. Nishiguchi, A. Fujiwara, and H. Yamaguchi, “Phonon Lasing in an Electromechanical Resonator,” Phys. Rev. Lett., Vol. 110, No. 12, p. 127202, 2013.
[17]	J. B. Khurgin, “Viewpoint: Phonon Lasers Gain a Sound Foundation,” Physics, Vol. 3, p. 16, 2010.
[18]	J. T. Mendonça, “Viewpoint: Lasers of Pure Sound,” Physics, Vol. 6, p. 32, 2013.
[19]	T. A. Palomaki, J. D. Teufel, R. W. Simmonds, and K. W. Lehnert, “Entangling Mechanical Motion with Microwave Fields,” Science, Vol. 342, No. 6159, pp. 710–713, 2013.
[20]	W. H. Zurek, “Decoherence and the Transition from Quantum to Classical,” Phys. Today, Vol. 44, No. 10, pp. 36–44, 1991.
[21]	W. Marshall, C. Simon, R. Penrose, and D. Bouwmeester, “Towards Quantum Superpositions of a Mirror,” Phys. Rev. Lett., Vol. 91, No. 13, p. 130401, 2003.
[22]	D. C. Burnham, and D. L. Weinberg, “Observation of Simultaneity in Parametric Production of Optical Photon Pairs,” Phys. Rev. Lett., Vol. 25, No. 2, pp. 84–87, 1970.
[23]	A. Einstein, B. Podolsky, and N. Rosen, “Can Quantum-mechanical Description of Physical Reality Be Considered Complete?”, Phys. Rev., Vol. 47, No. 10, pp. 777–780, 1935.
[24]	M. D. Reid and P. D. Drummond, “Quantum Correlations of Phase in Nondegenerate Parametric Oscillation,” Phys. Rev. Lett., Vol. 60, No. 26, pp. 2731–2733, 1988.
[25]	Z. Y. Ou and L. Mandel, “Violation of Bell’s Inequality and Classical Probability in a Two-photon Correlation Experiment,” Phys. Rev. Lett., Vol. 61, No. 1, pp. 50–53, 1988.
[26]	Y. H. Shih and C. O. Alley, “New Type of Einstein-Podolsky-Rosen-Bohm Experiment Using Pairs of Light Quanta Produced by Optical Parametric Down Conversion,” Phys. Rev. Lett., Vol. 61, No. 26, pp. 2921–2924, 1988.
[27]	J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics, Vol. 1, No. 3, pp. 195–200, 1964.
[28]	P. R. Tapster, J. G. Rarity, and P. C. M. Owens, “Violation of Bell’s Inequality over 4 km of Optical Fiber,” Phys. Rev. Lett., Vol. 73, No. 14, pp. 1923–1926, 1994.
[29]	A. K. Ekert, “Quantum Cryptography Based on Bell’s Theorem,” Phys. Rev. Lett., Vol. 67, No. 6, pp. 661–663, 1991.
[30]	E. Knill, R. Laflamme, and G. J. Milburn, “A Scheme for Efficient Quantum Computation with Linear Optics,” Nature, Vol. 409, No. 6816, pp. 46–52, 2000.
[31]	D. Bouwmeester, J. Pan, K. Mattle, M. Eibl, H. Weinfurter, and A. Zeilinger, “Experimental Quantum Teleportation,” Nature, Vol. 390, No. 6660, pp. 575–579, 1997.
[32]	A. N. Boto, P. Kok, D. S. Abrams, S. L. Braunstein, C. P. Williams, and J. P. Dowling, “Quantum Interferometric Optical Lithography: Exploiting Entanglement to Beat the Diffraction Limit,” Phys. Rev. Lett., Vol. 85, No. 13, pp. 2733–2736, 2000.
[33]	V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum-enhanced Measurements: Beating the Standard Quantum Limit,” Science, Vol. 306, No. 5700, pp. 1330–1336, 2004.
[34]	J. Q. You and Franco Nori, “Atomic Physics and Quantum Optics Using Superconducting Circuits,” Nature, Vol. 474, No. 7353, pp. 589–597, 2011.
[35]	B. Yurke, P. G. Kaminsky, R. E. Miller, E. A. Whittaker, A. D. Smith, A. H. Silver, and R. W. Simon, “Observation of 4.2-K Equilibrium-noise Squeezing via a Josephson-parametric Amplifier,” Phys. Rev. Lett., Vol. 60, No. 9, pp. 764–767, 1998.
[36]	M. A. Castellanos-Beltran, K. D. Irwin, G. C. Hilton, L. R. Vale, and K. W. Lehnert, “Amplification and Squeezing of Quantum Noise with a Tunable Josephson Metamaterial,” Nature Phys., Vol. 4, No. 12, pp. 929–931, 2008.
[37]	C. Eichler, D. Bozyigit, C. Lang, M. Baur, L. Steffen, J. M. Fink, S. Filipp, and A. Wallraff, “Observation of Two-mode Squeezing in the Microwave Frequency Domain,” Phys. Rev. Lett., Vol. 107, No. 11, p. 113601, 2011.
[38]	E. Flurin, N. Roch, F. Mallet, M. H. Devoret, and B. Huard, “Generating Entangled Microwave Radiation over Two Transmission Lines,” Phys. Rev. Lett., Vol. 109, No. 18, p. 183901, 2012.
[39]	C. A. Regal, J. D. Teufel, and K. W. Lehnert, “Measuring Nanomechanical Motion with a Microwave Cavity Interferometer,” Nature Phys., Vol. 4, No. 7, pp. 555–560, 2008.
[40]	T. Rocheleau, T. Ndukum, C. Macklin, J. B. Hertzberg, A. A. Clerk, and K. C. Schwab, “Preparation and Detection of a Mechanical Resonator Near the Ground State of Motion,” Nature, Vol. 463, No. 7277, pp. 72–75, 2009.
[41]	M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, “Cavity Optomechanics,” Rev. Mod. Phys., Vol. 86, No. 4, pp. 1391–1452, 2014.
[42]	T. A. Palomaki, J. D. Teufel, R. W. Simmonds, and K. W. Lehnert, “Entangling Mechanical Motion with Microwave Fields,” Science, Vol. 342, No. 6159, pp. 710–713, 2013.
[43]	S. G. Hofer, W. Wieczorek, M. Aspelmeyer, and K. Hammerer, “Quantum Entanglement and Teleportation in Pulsed Cavity Optomechanics,” Phys. Rev. A, Vol. 84, No. 5, p. 052327, 2011.
[44]	H. J. R. Westra, M. Poot, H. S. J. van der Zant, and W. J. Venstra, “Nonlinear Modal Interactions in Clamped-Clamped Mechanical Resonators,” Phys. Rev. Lett., Vol. 105, No. 11, p. 117205, 2010.
[45]	I. Mahboob, K. Nishiguchi, H. Okamoto, and H. Yamaguchi, “Phonon-cavity Electromechanics,” Nature Phys., Vol. 8, No. 5, pp. 387–392, 2012.
[46]	I. Mahboob, H. Okamoto, K. Onomitsu, and H. Yamaguchi, “Two-mode Thermal-noise Squeezing in an Electromechanical Resonator,” Phys. Rev. Lett., Vol. 113, No. 16, p. 167203, 2014.
[47]	D. Rugar and P. Grütter, “Mechanical Parametric Amplification and Thermomechanical Noise Squeezing,” Phys. Rev. Lett., Vol. 67, No. 6, pp. 699–702, 1991.
[48]	H. Okamoto, N. Kitajima, K. Onomitsu, R. Kometani, S. Warisawa, S. Ishihara, and H. Yamaguchi, “High-sensitivity Charge Detection Using Antisymmetric Vibration in Coupled Micromechanical Oscillators,” Appl. Phys. Lett., Vol. 98, No. 1, p. 014103, 2011.
[49]	S. C. Masmanidis, R. B. Karabalin, I. De Vlaminck, G. Borghs, M. R. Freeman, and M. L. Roukes, “Multifunctional Nanomechanical Systems via Tunably Coupled Piezoelectric Actuation,” Science, Vol. 317, No. 5839, pp. 780–783, 2007.
[50]	H. Okamoto, A. Gourgout, C. Chang, K. Onomitsu, I. Mahboob, E. Y. Chang, and H. Yamaguchi, “Coherent Phonon Manipulation in Coupled Mechanical Resonators,” Nature Phys., Vol. 9, No. 8, pp. 480–484, 2013.
[51]	J. D. Teufel, J. W. Harlow, C. A. Regal, and K. W. Lehnert, “Dynamical Backaction of Microwave Fields on a Nanomechanical Oscillator,” Phys. Rev. Lett., Vol. 101, No. 19, p. 197203, 2008.
[52]	F. Massel, T. T. Heikkilä, J. M. Pirkkalainen, S. U. Cho, H. Saloniemi, P. J. Hakonen, and M. A. Sillanpää, “Microwave Amplification with Nanomechanical Resonators,” Nature, Vol. 480, No. 7377, pp. 351–354, 2011.
[53]	N. Bergeal, F. Schackert, M. Metcalfe, R. Vijay, V. E. Manucharyan, L. Frunzio, D. E. Prober, R. J. Schoelkopf, S. M. Girvin, and M. H. Devoret, “Phase-preserving Amplification Near the Quantum Limit with a Josephson Ring Modulator,” Nature, Vol. 465, No. 7294, pp. 64–68, 2010.
[54]	C. C. Gerry and P. L. Knight, “Introductory Quantum Optics,” Cambridge University Press, Cambridge, England, 2005.
[55]	D. F. Walls and G. J. Milburn, “Quantum Optics,” Springer, 2008.
[56]	J. R. Johansson, N. Lambert, I. Mahboob, H. Yamaguchi, and F. Nori, “Entangled-state Generation and Bell Inequality Violations in Nanomechanical Resonators,” Phys. Rev. B, Vol. 90, No. 17, p. 174307, 2014.
[57]	H. Vahlbruch, M. Mehmet, S. Chelkowski, B. Hage, A. Franzen, N. Lastzka, S. Goßler, K. Danzmann, and R. Schnabel, “Observation of Squeezed Light with 10-dB Quantum-noise Reduction,” Phys. Rev. Lett., Vol. 100, No. 3, p. 033602, 2008.
[58]	The LIGO Scientific Collaboration, “Enhanced Sensitivity of the LIGO Gravitational Wave Detector by Using Squeezed States of Light,” Nature Photon., Vol. 7, No. 8, pp. 613–619, 2013.
[59]	F. Galve, L. A. Pachón, and D. Zueco, “Bringing Entanglement to the High Temperature Limit,” Phys. Rev. Lett., Vol. 105, No. 18, p. 180501, 2010.

	Imran Mahboob Senior Research Scientist, Distinguished Researcher, Hybrid Nanostructure Physics Research Group, NTT Basic Research Laboratories. He received an MPhys. in theoretical physics from the University of Sheffield, UK, in 2001 and a Ph.D. in physics from the University of Warwick, UK, in 2004. He joined NTT Basic Research Laboratories in 2005 and has been researching electromechanical systems to harness their nonlinear dynamics to develop phonon-based information technologies. He is a member of the Institute of Physics (IoP) and the American Physical Society (APS).
	Hajime Okamoto Senior Research Scientist, Hybrid Nanostructure Physics Research Group, NTT Basic Research Laboratories. He received a B.E., M.E., and a Ph.D. in materials science and engineering from Waseda University, Tokyo, in 1998, 2000, and 2004, respectively. He joined NTT Basic Research Laboratories in 2004 to research and develop semiconductor opto/electro-mechanical devices. He received an Outstanding Paper Award from the Japan Society of Applied Physics (JSAP) (2010), SSDM2009 Paper Award (2010), and the Young Scientists’ Prize (2014) from the Minister of Education, Culture, Sports, Science and Technology (MEXT). He is a member of JSAP.
	Hiroshi Yamaguchi Executive Manager of Quantum and Nano Device Research, Group Leader of Hybrid Nanostructure Physics Research Group, Senior Distinguished Researcher, NTT Basic Research Laboratories. He received a B.E. and a M.S. in physics and a Ph.D. in engineering from Osaka University in 1984, 1986 and 1993, respectively. He joined NTT Basic Research Laboratories in 1986 and studied compound semiconductor surfaces using electron diffraction and scanning tunneling microscopy. His current interests are micro/nanomechanical devices using semiconductor heterostructures. He was a visiting research fellow at Imperial College, University of London, UK, during 1995–1996 and a visiting researcher at the Paul Drude Institute, Germany, in 2003. He has been a guest professor at Tohoku University since 2006 and has served on more than 40 committees of academic societies and international conferences. He has received numerous awards including a JSAP Fellowship (2013), Commendation for Science and Technology by MEXT (2013), Inoue Prize for Science (2012), IoP Fellowship (2011), SSDM2009 Paper Award (2010), MNC2008 Outstanding Paper Award (2009), and Paper Awards from JSAP (1989, 2004, 2010). He is a member of JSAP, the Physical Society of Japan, IoP, APS, and the Institute of Electrical and Electronics Engineers.

↑ TOP