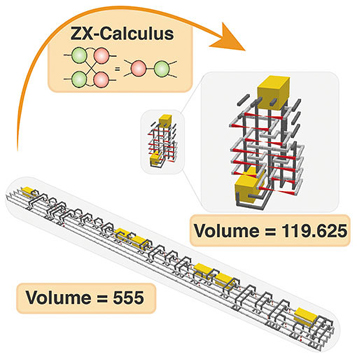
Effective Compression of Quantum Braided Circuits Aided by ZX-Calculus

1. Introduction

Researchers at the National Institute of Informatics (NII) and NTT proposed a compression method for reducing the resources associated with large-scale fault-tolerant quantum circuits that brings practical quantum computation one step closer to reality.

A major technical challenge for achieving practical quantum computation comes from the very need for a large number of physical qubits to prevent errors from accumulating during that computation. The consequence of this is that a fault-tolerant quantum circuit for a given computation requires a huge amount of resources, both in terms of qubits and computational time. In this work, published in Physical Review X on the 11th of November 2020 [1], they designed an efficient method of compressing such circuits with the purpose of decreasing their hardware demands. They used ZX-calculus as an intermediate language to reduce both the number of qubits and time required to execute such computation in many different circuits. With their method, they found an improvement of a 40% compression rate with respect to previous reductions, yielding compression rates higher than 70%. This method promises to open new venues of research in large-scale quantum computing and bring quantum computation closer to reality by relaxing its hardware demands.

2. Background

The fast-paced development of quantum technology has brought quantum computing into the era of noisy intermediate-scale quantum (NISQ) devices, which have served as the platform for early proof-of-principle experiments. However, they are still prone to errors, which significantly accumulate during their operation. To obtain a truly practical quantum advantage, the design of a fully operational large-scale quantum computer with high-error tolerance is required. Current cutting-edge technology allows us to engineer NISQ devices with approximately 100 qubits, while fault-tolerant computers are expected to require millions of physical qubits at least to encode the logical information with sufficiently low error rates. This difference in size is currently the main obstacle to the development of large-scale fault-tolerant quantum computers.

Progress in hardware technology is expected to bring scalability into quantum computer chip manufacturing and qubit controls. However, it is also possible for software to reduce the cost associated with fault-tolerant quantum computation implementations. Large-scale quantum computers will consist of many technological layers from the application level all the way down to the hardware, which will require various rounds of compilation and optimization. The resource cost will then come from the layers where quantum error correction codes are introduced to provide fault-tolerance for the implementation of the circuit. For most current quantum-computer architectures, topological error-correcting codes are preferred, in particular the surface code is expected to be used for superconducting-qubit-based quantum computers where lattice-surgery or braiding is chosen for logical gate operations, the latter being ideally suited to distributed quantum computation. A fault-tolerant implementation of quantum computational circuits not only makes the quantum computer larger but also the runtime longer. “These operations require a high level of external control over quite an extended time. In turn, this means the computation is more susceptible to errors,” says Michael Hanks from NII. Therefore, the possibility of compressing quantum circuits at the logical level not only implies a huge saving for the time and resources needed for quantum computation but also lower errors. “Once a quantum algorithm or computation is compiled into a fault-tolerant circuit, to reduce both the amount of time and space required is paramount to bring practical quantum computers closer to reality,” says Marta Estarellas from NII. Thus far, there has been no established approach to tackle this problem, and effective methods to treat these logical gate circuits have not been formulated.

3. Research results

As mentioned above, their method is used for compressing braided fault-tolerant circuits on the three-dimensional (3D) topological code. Braided circuits are generally represented as 3D structures, a low-level close-to-hardware language whose main elements consist of tubes or pipes that represent the defects or logical qubits. A quantum gate circuit can be represented as interlacing pipes. By manipulating these pipes, the quantum gate circuit can be compressed. The main problem in braided circuit reduction is that there are few ad-hoc rules to manipulate these pipes. The first piece of this puzzle is to use ZX-calculus, a language that is equipped with a complete set of rules to manipulate logical gate circuits, to carry out this compression. However, we still need to solve another piece of the puzzle to harness ZX-calculus, and that is discovering the translation relations between ZX-calculus and the components of the braided circuit. The researchers have shown that these two representations of logical gate circuits can be mapped one to another by identifying a new interpretation hidden in ZX-calculus. After testing their compression method against a set of test circuits, they were able to reduce those circuit volumes by approximately 70% on average (Fig. 1).

Fig. 1. Compression of a quantum circuit with a 77.4% reduction rate.

Their method also allows unification of the two main operation models used in surface-code-based computation: lattice-surgery and braiding. “This unification promotes ZX-calculus from a representation of quantum logical circuits to a quantum computer language. We can now think about designing computer languages and compliers in the logical operation layer of the technological stack,” says William J. Munro from NTT. Importantly, the unification of these two models also contributes directly to compression. Taking the hybrid compilation approach, we can compress a circuit further, beyond what each individual method had achieved.

4. Methods

Previous methods for fault-tolerant quantum circuit compression have suffered from the complexity of trying to reduce circuits directly in the 3D representation. One of the key contributions of this new method is the inclusion of ZX-calculus as an intermediate language to minimize the circuit volume. This diagrammatic language can be used to represent quantum processes and circuits in the form of tensor networks with a limited set of elements or nodes. This language can then apply a set of transformation rules (axioms) to change the structure of the network without modifying its underlying mathematical meaning (hence its operation). These transformation rules can be carefully applied in such a way that the total number of nodes is reduced. As the set of transformations is complete, any minimal structure can be reached in principle. The compressed circuit in ZX-calculus is then mapped to the braided circuit by applying the newly identified relation between them.

5. Outlook

Global efforts are pushing quantum technology ahead rapidly with a steadily increasing number of qubits present in each next-generation chip. Nevertheless, in the race to achieve practical quantum computing, it is not enough to just improve the hardware. Software techniques can significantly reduce the requirement for quantum computer hardware, which can bring the development of fault-tolerant quantum computers forward by years. “The logical gate layer situates in the middle of the quantum computer technology stack, and our method can serve as a basis to further develop instruction set architectures and design quantum compliers,” adds Kae Nemoto from NII.

6. Funding

This research was made possible thanks to the support of the Japanese Ministry of Education, Culture, Sports, Science and Technology Quantum Leap Flagship Program (MEXT Q-LEAP) JPMXS0118069605.

Reference

[1]	M. R. Hanks, M. P. Estarellas, W. J. Munro, and K. Nemoto, “Effective Compression of Quantum Braided Circuits Aided by ZX-Calculus,” Phys. Rev. X, Vol. 10, No. 4, 041030, Nov. 2020.

For inquiries:

Public Relations, NTT Science and Core Technology Laboratory Group

https://www.ntt.co.jp/news2020/2011e/201112a.html?_ga=2.111847364.1583916423.1614580614-1319211474.1585803734

↑ TOP