|
|||||||||||||||||
|
|
|||||||||||||||||
|
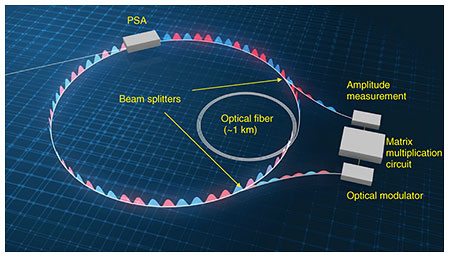
Feature Articles: Toward New-principle Computers Vol. 19, No. 5, pp. 18–22, May 2021. https://doi.org/10.53829/ntr202105fa2 Performance Comparison between Coherent Ising Machines and Quantum AnnealerAbstractNTT has been developing a coherent Ising machine (CIM), which efficiently finds solutions to ground-state-search problems of the Ising model using a network of optical parametric oscillators. We introduce our recent experiment that compared the computational performance of CIMs (the one developed by NTT and another developed by Stanford University) with a quantum annealer, which solves the Ising-model problems using superconducting devices. Keywords: coherent Ising machine, quantum annealing, LASOLV 1. IntroductionA combinatorial optimization problem is to find the best combination of choices among a set of many choices and is generally considered a problem that cannot be efficiently solved with modern digital computers. It is known that any combinatorial optimization problem can be efficiently converted to a ground-state-search problem of the Ising model, which is a theoretical model describing the behavior of interacting spins. A recent trend is to solve such Ising model problems through experiments using physical systems that mimic the Ising spins, which are now called Ising machines. A pioneer of such Ising machines is the quantum annealer (QA) based on superconducting qubits as artificial spins. The Canadian company D-Wave Systems has developed QAs with as many as thousands of qubits [1]. A coherent Ising machine (CIM) is another Ising machine that uses degenerate optical parametric oscillators (DOPO) as spins [2, 3]. NTT has been developing a computation system based on the concept of a CIM called LASOLVTM [4]. In this article, we describe the experimental performance comparison between CIMs and a D-Wave QA undertaken by NTT, National Aeronautics and Space Administration (NASA), and Stanford University [5]. 2. Coherent Ising machineA DOPO is an optical oscillator that can be implemented by placing a phase sensitive-amplifier (PSA) in an optical cavity. A PSA is an optical amplifier based on optical parametric amplification and efficiently amplifies the 0 and π phase components relative to the pump phase [6]. As a result, a DOPO takes only the 0 or π phase above the oscillation threshold; thus, the discrete phase states can be used to represent the Ising spin states. The CIM developed by NTT generates thousands of time-multiplexed DOPO pulses by turning on and off the PSA placed in a 1-km optical fiber with a 1-GHz frequency (Fig. 1). The interaction between the DOPO pulses are implemented using a method called measurement-feedback. With this method, some of the pulse energies of N DOPO pulses are split using a beam splitter for each circulation in the cavity, and the amplitudes (with signs) of all N DOPO pulses are measured. The measurement results are input into a digital circuit for matrix computation, where the spin-spin interaction matrix (an N × N matrix) for a given Ising problem is installed in advance. The digital circuit multiplies the matrix and set of N measurement results to obtain the feedback signal for each pulse in the next circulation in the cavity. We then use the feedback signal to modulate an optical pulse, and the pulse is injected into the corresponding DOPO pulse inside the cavity through another beam splitter to complete measurement-feedback. By repeating this procedure typically during 100 to 1000 circulations in the cavity while increasing the pump amplitude from zero, the combination of the DOPO phases evolves into a phase that most stabilizes the whole system, which in many cases corresponds to the ground state of the given Ising problem. In 2016, we reported on a 2000-node CIM on the basis of measurement-feedback and demonstrated that the CIM could deliver a fine solution to a 2000-node optimization problem ~50 times faster than simulated annealing implemented on a modern digital computer [2].
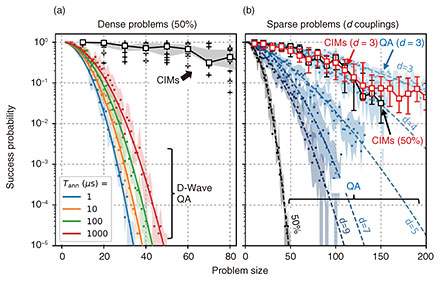
3. Performance comparison with D-Wave QAA quantum annealing algorithm starts with an initial state where all the spins are set at the superposition of spin up and down by applying transverse magnetic fields. Spin-spin interactions for a given Ising problem are then gradually implemented while decreasing the transverse field. With the help of quantum fluctuations, the whole system reaches ground states with high probability [7]. The D-Wave QA has been used in several proof-of-concept experiments such as optimization of traffic flow [8]. We report on an experiment of comparing the probabilities to obtain the exact solutions to the common Ising model problems obtained with the CIM developed by NTT and that developed by Stanford University and the 2000-spin D-Wave QA owned by NASA [5]. We denote the number of spins for a given problem, average number of couplings per spin, and coupling density as N_p, d, and D (= d/N_p), respectively. The success probabilities for the problems with D = 50% as a function of N_p are shown in Fig. 2(a). While the success probability of the CIMs did not decrease significantly with the problem size, that for the D-Wave QA decreased rapidly as we increased N_p and ended up at 0.001% with N_p = 50. Figure 2(b) shows the relationship between the success probabilities and d. When solving sparse problems with d = 3, the D-Wave QA slightly outperformed the CIMs. However, the performance of the D-Wave QA degraded rapidly when N_p increased. The success probabilities for d = 3 and D = 50% were comparable, indicating that success probability does not depend on D.
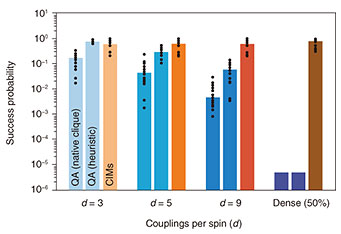
The performance difference between the CIMs and D-Wave QA probably originates from the difference in the implementation of the spin-spin couplings. The superconducting qubits of the D-Wave QA are physically connected in a graph structure called a Chimera graph, where each qubit has only six connections. Therefore, a given Ising problem needs to be converted to a problem on the Chimera graph structure before being input into the D-Wave QA, which often increases the number of required spins, especially when solving dense problems. On the other hand, all-to-all coupling among DOPO pulses is possible in the CIMs because of the use of measurement-feedback; thus, Ising problems with any coupling density can be input without any conversion. In our experiment, we used two methods for converting Ising problems into the Chimera graph structure. One is the native clique embedding method, which embeds a problem into the Chimera graph in accordance with a pre-determined algorithm. The other is a heuristic method that undertakes optimization to minimize the required number of qubits in advance for each problem. The success probabilities of the D-Wave QA on the basis of these two embedding methods and that for the CIMs for 50-node Ising problems are shown in Fig. 3. The use of the heuristic method could decrease the effective problem size run on the D-Wave QA, improving success probabilities compared with native clique embedding. Nevertheless, the success probabilities of the D-Wave QA did not reach that of the CIMs when d was 5 or larger, and the difference increased as d or D increased. This suggests that the manner of implementing the Ising model problems onto a physical system significantly affects the computational performance of Ising machines based on such systems.
4. SummaryWe described the performance comparison between CIMs and the D-Wave QA (as of 2019). We expect that both will evolve and improve in performance. Important future work regarding these computers is to clarify if such new computers based on physical systems can have an advantage over modern digital computers and if such an advantage can lead to applications that benefit society. References
|
|||||||||||||||||