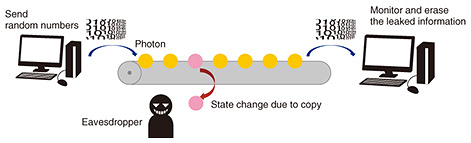
Improving the Performance of Quantum Key Distribution

1. Basics of quantum key distribution and research in NTT

It is necessary to encrypt information for secure communications via the Internet. For example, malicious eavesdropper can read information about a credit card if we send it without encryption. Public-key cryptography, such as Rivest–Shamir–Adleman (RSA), is used for this purpose. Its security is based on a problem that is difficult to solve using a modern digital computer, so called computational security. However, a quantum computer having error correction capability can break RSA efficiently. There is another encryption called one-time pad, which is a common-key cryptography. This cryptography uses the fact that a third party does not have enough information to break the encryption. Such an information-theoretic security cannot be broken by any type of computer. Despite its strong encryption, it has a serious disadvantage in that it is difficult to create a situation in which the third party does not have enough information. We use a bit represented by 0 and 1 in a communication system. To make one-time pad ultimately secure, only the legitimate users for the communications need to share random numbers^*1 (secret key), the length of which is equal to the bit length of the information they really want to send. If we can send the secret key securely, one-time pad looks useless because, in a rough consideration, we can directly send the information using such a secure method used for sharing the secret key instead of one-time pad.

Quantum key distribution (QKD) is a technique that solves this problem. QKD uses the fact that an attempt to clone a quantum state changes the original state (Fig. 1). By monitoring such a change in the state, we can estimate how much information was leaked during communications. We cannot directly send a massage we want to encrypt because we cannot prevent the message from being leaked. However, if we send random numbers having no meaningful information, we can generate a secret key by erasing the leaked information from the shared random numbers after the communication. By using this secret key for one-time pad, we can enable unbreakable secret communications.

Fig. 1. Schematic diagram of QKD.

While we often hear about QKD on the news, it has been studied since its invention in 1984 [1]. NTT has continued its long-term research on QKD [2], such as security analysis, experimental demonstration, and the proposal of our unique QKD protocol called differential phase shift QKD. Let us introduce our recent activities on high-dimensional QKD and a technology for improving its error robustness.

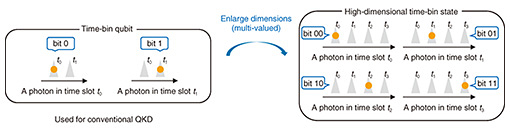
2. High-dimensional QKD and scalable measurement device

High-dimensional QKD uses a high-dimensional quantum state to enhance the secret-key rate, which corresponds to the communication speed of QKD. A conventional QKD system uses a quantum bit (qubit) representing 0 or 1. In our research group, we use a time-bin qubit, 0 or 1 of which are represented by two temporal positions of a photon^*2 (Fig. 2 left). If we can encode multiple values, such as 0, 1, 2, …, instead of a bit value, we can increase the amount of information per photon (Fig. 2 right). A high-dimensional state is such a state representing multiple values and its concept is similar to pulse amplitude modulation (PAM)^*3 and quadrature amplitude modulation (QAM)^*4 used in modern optical communications. A very high-speed secret-key generation of 26.2 Mbit/s has been reported by using four-dimensional time-bin states represented by four temporal positions [3].

Fig. 2. Schematic diagram of time-bin state.

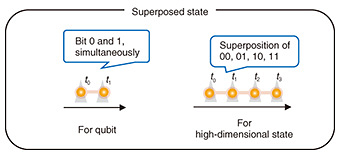
As we explained in the previous section, it is important to estimate how much information of random numbers was leaked for generating a secure secret key. For this purpose, QKD uses superposed states. A superposed state is a state in which we cannot essentially determine 0 or 1 for a qubit and 0, 1, 2, … for a high-dimensional state (Fig. 3). We can estimate the amount of leaked information by using superposed states that satisfy a special relation called mutually unbiased. In a d-dimensional system, we can use at most (d + 1) measurements, which satisfy such a special relation. An experiment using two types of measurements to estimate the amount of leaked information achieved 26.2-Mbit/s secret key generation [3]. By using (d + 1) measurements, we can more precisely evaluate the change in the quantum state during communications. Therefore, we can more precisely estimate the amount of leaked information, which results in an improvement in the secret-key rate. In other words, multiple measurements make a high-dimensional QKD system more robust against errors.

Fig. 3. Schematic diagram of superposed state.

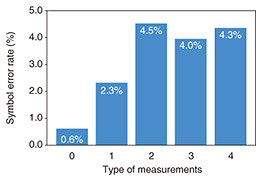
NTT developed and demonstrated an implementation of a scalable measurement device of (d + 1) measurements for high-dimensional time-bin states [4]. A measurement for time-bin states uses delay Mach-Zehnder interferometers (MZIs)^*5 and single-photon detectors. In an implementation of a previous measurement device, (d − 1) MZIs and (d + 1) single-photon detectors were required even for two measurements [3]. By using the above scalable measurement device, all the (d + 1) measurements for d = 2^N can be implemented using N MZIs and three single-photon detectors independent of d (Fig. 4). We conducted experiments involving five measurements for four-dimensional time-bin states. The experimental results indicated error rates lower than the threshold required to generate a secret key (Fig. 5). Hence, we expect that this device can be used for a high-dimensional QKD system that is more robust against errors.

Fig. 4. Measurement device for four-dimensional time-bin states.

Fig. 5. Experimental results of error rate.

3. Extension of the security proof

In the previous section, we explained that (d + 1) measurements can be used for a robust high-dimensional QKD system. However, a rigorous security of this QKD protocol was proven only if d is a prime number (2, 3, 5, …). Therefore, we cannot directly apply that security proof for a four-dimensional system with the above scalable measurement device. To circumvent this problem, we also extended the previous security proof [5] for prime power dimensions (e.g., d = 2, 4, 8, and 3, 9, 27). In this security proof, we use operators that describe operations on a quantum state. Corresponding to the operators used in the previous security proof, there is a generalized operator using the Galois field^*6, which is used in, e.g., coding theory [6]. Because we can use the Galois field as long as d is a prime power, we could extend the previous security proof by using these generalized operators for prime-power dimensions. Therefore, we can use the scalable measurement device for a four-dimensional QKD system to ensure rigorous security.

4. Toward a practical QKD system

We introduced high-dimensional QKD and a scalable measurement device to enhance the error robustness as recent activities in NTT to improve the performance of QKD. We conducted a proof-of-principle experiment on generations and measurements of high-dimensional quantum states for such a QKD system. To implement a practical QKD system, we also need to consider other problems, for example, a finite key analysis which is a detailed treatment of statistical errors due to a finite number of measurement results. It is also important to explore other applications of the scalable measurement device because the mutually unbiased relation can be found in quantum communications and information processing other than QKD. Although we introduced only the approach of using a high-dimensional state in this article, NTT will continue to conduct research on other approaches toward practical quantum information technologies.

References

[1]	C. H. Bennett and G. Brassard, “Quantum Cryptography: Public Key Distribution and Coin Tossing,” Proc. of IEEE International Conference on Computers Systems and Signal Processing, pp. 175–179, Bangalore, India, 1984.
[2]	“Feature Articles: Quantum Cryptography,” NTT Technical Review, Vol. 9, No. 9, 2011. https://ntt-review.jp/archive/2011/201109.html
[3]	N. T. Islam, C. C. W. Lim, C. Cahall, J. Kim, and D. J. Gauthier, “Provably Secure and High-rate Quantum Key Distribution with Time-bin Qudits,” Sci. Adv., Vol. 3, No. 11, e1701491, 2017. https://doi.org/10.1126/sciadv.1701491
[4]	T. Ikuta, S. Akibue, Y. Yonezu, T. Honjo, H. Takesue, and K. Inoue, “Scalable Implementation of (d + 1) Mutually Unbiased Bases for d-dimensional Quantum Key Distribution,” Phys. Rev. Res., Vol. 4, No. 4, L042007, 2022. https://doi.org/10.1103/PhysRevResearch.4.L042007
[5]	L. Sheridan and V. Scarani, “Security Proof for Quantum Key Distribution Using Qudit Systems,” Phys. Rev. A, Vol. 82, No. 3, 030301(R), 2010. https://doi.org/10.1103/PhysRevA.82.030301
[6]	T. Durt, B.-G. Englert, I. Bengtsson, and K. Życzkowski, “On Mutually Unbiased Bases,” Intl. J. Quantum Inf., Vol. 8, No. 4, pp. 535–640, 2010. https://doi.org/10.1142/S0219749910006502