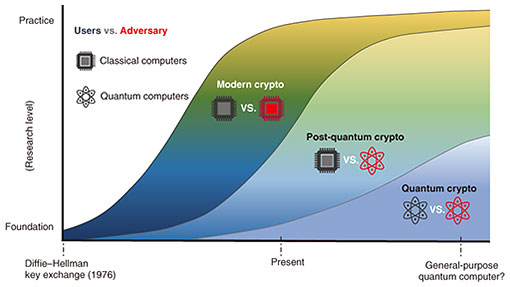
Development of Modern Cryptography and Research on Quantum Cryptography

1. Cryptographic research at NTT

NTT’s research on cryptography, which began in 1982 with a bank card forgery incident involving an employee of Nippon Telegraph and Telephone Public Corporation, has lasted more than 40 years. In 1992, the Cryptography Research Team, which initially included only three members, became an official research group of eight members within the Information and Communication Network Laboratories. Along with the emergence of the Mosaic web browser in 1993, the Internet exploded, leading to the recognition of the importance of information security. In response to these developments, the group was reorganized as the Information Security Project in 1999 then as NTT Secure Platform Laboratories in 2012. Today, information security technologies have become commoditized to support daily life. Now known as NTT Social Informatics Laboratories, the research group continues to engage in a wide range of research on cryptography and information security.

Advanced networks have enabled the operation of various information distribution systems. The scope of cryptography has expanded from a basic defensive stance centered on concealment and authentication to an offensive stance of creating applications for cryptocurrency, cloud computing, and other new areas. With the increased likelihood of achieving general-purpose quantum computers, it has also become clear that public-key cryptosystems currently in use will rapidly become compromised. Therefore, new measures are now needed for defense purposes. The creation of cryptographic applications that proactively use general-purpose quantum computers and the establishment of the fundamental theories underpinning them will likely become a reality.

This article discusses modern cryptography, in which both system users and attackers use currently available classical computers; quantum-resistant cryptography, in which only attackers use quantum computers; and quantum cryptography, in which both users and attackers use quantum computers (Fig. 1). An overview of topics mainly related to public-key cryptography and its relationship with NTT’s cryptographic theory research is provided. Another important research topic, symmetric-key cryptography, is discussed in terms of quantum-resistant cryptography.

Fig. 1. Development from modern to quantum cryptography.

2. Advances in modern cryptography

Secure and efficient cryptographic schemes are constructed on the basis of computational assumptions that it is, on average, difficult to solve a particular class of problems with a probabilistic Turing machine. However, as the algorithms and hardware available to the adversaries become more advanced, individual problems can be solved in less time than before. When this occurs, cryptographic schemes based on that class of problems would require larger keys for security, thus degrading performance. Rivest–Shamir–Adleman (RSA) encryption in 1977, Rabin encryption in 1978, and ESIGN (Efficient Digital Signature) system developed by NTT in 1990 take advantage of the hardness of the prime factorization problem. RSA’s public key was considered secure at 512 bits at the time of its development, but now at least 3072 bits are recommended [1]. Diffie–Hellman key exchange in 1976, ElGamal encryption in 1985, and DSA (Digital Signature Algorithm) signature in 1993, which are also pioneering cryptographic techniques, were initially constructed using the discrete logarithm problem over multiplicative groups but have transitioned into instantiations based on the elliptic-curve discrete logarithm problem (such as ECDSA (Elliptic Curve Digital Signature Algorithm) signature in 2005), which enables a smaller public key at the same security level.

As networks advance, advanced cryptographic applications such as cloud computing have emerged. Cryptography has evolved from technologies for traditional purposes, such as information hiding and authentication, to more valuable technologies for constructing advanced information-sharing services. Bilinear mapping (pairing) over elliptic curve groups was first used for secure key generation by Kalisky, Jr. in 1987. It became widely known through the security analysis of the elliptic curve cryptography (MOV (Menezes–Okamoto–Vanstone) reduction) by Tatsuaki Okamoto of NTT and co-researchers in 1991. Since then, it has been widely used for cryptography in identity (ID)-based key exchange (Ogishi et al., 2000) and ID-based cryptography (Boneh et al., 2001), and has generated many practical applications to date. In particular, non-interactive zero-knowledge proofs, the practical value of which had been limited until then, have rapidly expanded with pairing-based constructions (Groth et al., 2008). At NTT, research has also progressed on structure-preserving cryptography (Abe et al., 2009), which enables advanced functions by freely combining cryptographic schemes over pairing groups. Pairing technology has contributed significantly to the realization of the advanced concept of computationally sound proof (Micali, 2000), which enables efficient verification of complex statements with a short proof, in the form of the Zero-Knowledge Succinct Non-interactive Argument of Knowledge (zk-SNARK) (Gennaro et al., 2012). Since short proofs are highly demanded in blockchain applications, zk-SNARK is foreseen to become the foundation technology for the Web3 era. Its usefulness is rapidly improving with the development of front-end compilers that translate statements in high-level languages such as C++ into an NP (non-deterministic polynomial time)-complete intermediate language that the back-end zk-SNARK can handle.

With the deployment of cryptography in various information systems and the advancement of the functionality of cryptography, the notion of security has also become more sophisticated. Proofs based on relatively simple security notions such as indistinguishability have been typically demonstrated by a simple reduction to a hardness assumption; it includes the Blum–Micali pseudo-random generator based on the discrete logarithm problem in 1982 and Rabin encryption based on the integer factorization problem in 1986. Higher levels of security have complicated the security proofs and constructions. In the well-known security notion of indistinguishability against adaptive chosen ciphertext attacks (IND-CCA) security (Bellare and Rogaway, 1991), an adversary is allowed to participate more actively in the input and output of cryptosystems. The random oracle paradigm introduced by Bellare et al. in 1993, which idealized hash functions, contributing significantly to simplifying construction and security proofs. Various encryption schemes and applications demonstrated as secure in the random oracle model were proposed from the late 1990s into the 2000s, leading to the spread of the paradigm of provable security. At NTT, the Fujisaki–Okamoto (FO) transformation in 1998, PSEC-KEM (Provably Secure Elliptic Curve encryption with Key Encapsulation Mechanism) in 1999, and the message-recovery signature scheme ECAOS (Elliptic Curve Abe–Okamoto–Suzuki signature) in 2008 have been developed in the random oracle model. However, many studies have been conducted to pursue efficient, provable, and secure constructions that do not rely on random oracles.

The cryptographic techniques developed for today’s computers and networks will continue to be passed down as foundations, providing insight into the construction of secure cryptography even in a post-quantum computer world, as discussed below.

3. From modern cryptography to post-quantum cryptography

It is believed that it will take a considerable amount of time before adversaries can use general-purpose quantum computers. However, since most of the present information in circulation is being collected and accumulated, cryptographic technologies deployed now need to withstand future attacks using general-purpose quantum computers to ensure privacy of the accumulated information. Lattice-based problems are promising as basic hardness assumptions to be used in constructing post-quantum secure cryptography. The use of the lattice problem in cryptography began with the construction of a one-way function by Ajtai in 1996. Subsequently, a lattice-based, concretely efficient N-th degree Truncated polynomial Ring Units (NTRU) encryption was proposed in 1998. For digital signatures, constructions based on multivariate polynomials and hash functions are also promising options to achieve post-quantum security.

In the Post-Quantum Cryptography (PQC) Competition launched by the U.S. National Institute of Standards and Technology (NIST) in 2017, open calls for quantum-computer-safe public-key cryptosystems and digital signatures were made, and the final candidates were announced in 2022. This means that post-quantum cryptography is rapidly approaching practical application. It will become the new standard by 2024 and is expected to replace the current ones by 2030. NTT has contributed to the competition as a proponent of NTRU encryption and in evaluating many candidates. Since quantum computers can operate over superposition states, and the computational principles of the adversaries differ, techniques for the security proofs have been reconstructed to match quantum computers. The aforementioned FO transformation has also been re-examined so that safety can be established in a quantum random oracle model that executes computations in the quantum state. FO transformation is used to make CRYSTALS-Kyber, the cryptographic scheme adopted in the NIST PQC competition, IND-CCA secure.

Lattice-based cryptography is fundamental for developing advanced cryptosystems, aside from being quantum-safe. Fully homomorphic encryption, which enables addition and multiplication on encrypted plaintext, is an essential cryptographic technology with a wide range of applications, including cloud computing. NTT has been engaged in security analysis of lattice-based cryptography and research on fully homomorphic encryption since 2013.

By doubling or tripling the key length and block size, symmetric-key cryptography, such as block ciphers and hash functions, can be secured against key search attacks that use general-purpose quantum algorithms irrespective of their internal structures. Thus, unlike public-key cryptography based on number-theoretic assumptions, they are thought to be impervious to the fatal consequences of such attacks. Attacks by quantum computers also pose a new risk for symmetric-key cryptography because they have been shown to be effective against specific well-known structures. The feature article in this issue entitled “Security of Hash Functions against Attacks Using Quantum Computers” [2] explains the security of hash functions against attacks using quantum computers, particularly, the quantum resistance of SHA-2.

Although research on post-quantum zero-knowledge proofs and cryptographic protocols is also advancing, further research is needed to promptly replace current technologies. For example, in anonymous electronic voting, the size of one vote in conventional classical cryptography will expand from a few kilobytes to several hundred kilobytes in quantum-safe voting systems. These technologies are essential for the transition to quantum-resistant security of information distribution systems based on current encryption technologies, and are expected to develop at an early stage.

4. Toward quantum cryptography

The remarkable increase in computing power of edge devices has made a variety of applications possible. When quantum computers will be widely used not only by adversaries but also by ordinary users, what technologies and applications would be possible? Quantum physicist Stephen Wiesner described the idea of applying the loss of quantum states by observation into creating unforgeable quantum money in 1969. (Current anti-counterfeiting of cryptocurrencies and e-money relies on online verification by transaction registers, post-detection by cryptography, or tamper resistance in a trusted execution environment.) Although current digital technologies can prove that information is stored, they cannot prove that it has been deleted. This makes the disposal of information uncertain and creates the risk of information leakage. The feature article entitled “Functional Encryption Enabling Secure Leasing of Private Keys” [3] introduces research for proving that cryptographic private keys have been deleted. Now that quantum computers have become a common topic, not only are new applications sought, but research is also being conducted to integrate quantum physics, quantum information processing, and cryptography with the aim of establishing the basic theories. The feature article entitled “Quantum Algorithms with Potential for New Applications” [4] introduces research demonstrating quantum superiority, i.e., how the computational power of quantum computers surpasses current computers for certain tasks.

5. Conclusion

In this article, an overview of NTT’s research on cryptography from the viewpoint of the development of quantum computers was presented. NTT Social Informatics Laboratories will continue to conduct research on a variety of topics, from foundations of cryptography, which will continue to be important as a basis of information sharing, to exciting applications far into the future. Going forward, we will continue to deploy technologies that will contribute to information distribution in the present as well as in the future.

References

[1]	Cryptography Research and Evaluation Committees, “CRYPTREC Ciphers List,” https://www.cryptrec.go.jp/en/list.html
[2]	A. Hosoyamada, “Security of Hash Functions against Attacks Using Quantum Computers,” NTT Technical Review, Vol. 21, No. 7, pp. 43–47, July 2023. https://ntt-review.jp/archive/ntttechnical.php?contents=ntr202307fa4.html
[3]	R. Nishimaki, “Functional Encryption Enabling Secure Leasing of Private Keys,” NTT Technical Review, Vol. 21, No. 7, pp. 33–37, July 2023. https://ntt-review.jp/archive/ntttechnical.php?contents=ntr202307fa2.html
[4]	T. Yamakawa, “Quantum Algorithms with Potential for New Applications,” NTT Technical Review, Vol. 21, No. 7, pp. 38–42, July 2023. https://ntt-review.jp/archive/ntttechnical.php?contents=ntr202307fa3.html