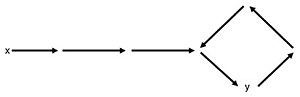
Arithmetic Problems in Dynamical Systems

1. Introduction

A system in which points move according to a certain rule over time is called a dynamical system. Given a polynomial or a rational map f, we consider the orbit of each point under iterated composition, that is,

z f(z) f(f(z)) = f ²(z) f(f(f(z))) = f ³(z)

Regarding this sequence as a discrete time series, we obtain a dynamical system. The questions of when this sequence diverges to infinity or converges to a certain value are fundamental yet challenging. Arithmetic dynamics studies arithmetic phenomena in such dynamical systems and was established around 2000 by Silverman. Depending on whether the focus is more on number theory or dynamical systems, the nature of the research varies. This article introduces arithmetic dynamics from a number theoretic perspective, particularly problems related to the determination of rational points on curves. Problems from the dynamical-systems perspective are introduced in another article [1] in this issue.

One major goal in arithmetic dynamics is to complete the dictionary of analogies between the theory of elliptic curves or their higher-dimensional analogs, Abelian varieties in number theory, and their dynamical system counterparts. Through the dictionary, one often obtains new insights into arithmetic geometry.

2. Morton–Silverman conjecture

A torsion point on an elliptic curve is a point that becomes the identity element O under repeated addition. This is equivalent to a point where the orbit under the iterated composition of the doubling map is a finite set. When an elliptic curve is defined over rational numbers, Mazur proved that there are at most 16 such rational points (more precisely, he completely determined the possible group structures) [2].

What about, for example, the iteration of the map z² on the complex plane? The points, the orbits under z² of which are finite in the complex domain, are the roots of unity and 0. Among these, the rational points (rational preperiodic points) are only 0, 1, and –1. What about the map ? The rational preperiodic points in this case are only and Is the finiteness of rational preperiodic points special to these maps? In fact, it can be proven that the number of rational preperiodic points is finite for any polynomial with rational coefficients of degree d ≥ 2. However, is the number of such points as small as 3 or 4? When restricted to rational periodic points, i.e., rational points with periodic orbits, what periods are possible? The following conjecture addresses this.

Morton–Silverman uniform boundedness conjecture (special case): For any integer d ≥ 2, there exists a constant N_d such that the number of rational preperiodic points of any rational function f of degree d is at most N_d.

This conjecture remains largely open even for quadratic polynomials z² + c (with c a given rational number). It is relatively easy to prove that there are infinitely many cs for which there are rational periodic points z of periods 1, 2, and 3. However, it has been shown that there are no cs for which z² + c allows rational periodic points of periods 4, 5, or 6 (with the 6-period case requiring the assumption of the Birch–Swinnerton-Dyer (BSD) conjecture) [3–5]. Assuming a generalized abc conjecture, it has been proven that z² + c does not have rational periodic points of period 4 or higher. One might think of solving the equation f_cⁿ(z) = z to find rational periodic points of period n. For n = 4, for example, one would consider the solutions of the polynomial obtained by dividing f_c⁴(z) – z by f_c²(z) – z. The situation is similar for general period n. The resulting polynomials are called the n-th dynatomic polynomials. The figure X_n^dyn defined by these polynomials is a curve, and the problem reduces to determining the rational points on this curve. These problems are familiar to those aware of Fermat’s Last Theorem. In fact, for n = 4, 5, 6, the results are proven using theories developed for determining rational points on specific curves, fully using techniques built up until the solution of Fermat’s Last Theorem. However, it should be noted that the key theory that led to the final proof of Fermat’s Last Theorem is not about determining rational points on specific curves. By using a non-trivial rational solution of Fermat’s Last Theorem, a too-nice elliptic curve called the Frey curve is defined. According to the Taniyama–Shimura conjecture, which is now a theorem, any elliptic curve corresponds to a modular form [6, 7]. However, due to the properties of the original elliptic curve, the corresponding modular form has such too-nice properties that it can be shown not to exist, leading to a contradiction. Therefore, Fermat’s Last Theorem’s non-trivial solution does not exist. While it is natural to explore if this surprising method can be applied to the Morton–Silverman conjecture, no method, such as for defining a Frey curve, has been developed.

As mentioned above, Mazur proved that the number of rational torsion points on an elliptic curve is at most 16, but what about the higher-dimensional case, such as Abelian varieties? This problem remains open even for the two-dimensional case. Fakhruddin has shown that this conjecture follows from the Morton–Silverman conjecture, indicating a significance beyond merely following analogies [8].

3. Dynamical cancellation

Consider the following scenario related to the Morton–Silverman conjecture. Let f be a polynomial of degree d. Suppose f has a rational preperiodic point x. Such a point will eventually enter a periodic orbit after certain iterations of f. Suppose it enters a periodic orbit of period 4 at time 3, as illustrated in the orbit diagram (Fig. 1). In this case, let y = f ⁴(x). Then, x and y collide at time 3. That is, f ²(x) ≠ f ²(y) and f ³(x) = f ³(y). For a fixed rational map f, how many rational pairs (x, y) satisfy f ^n–1(x) ≠ f ^n–1(y) and f ⁿ(x) = f ⁿ(y)? This question is called dynamical cancellation. To answer this, one could examine the existence of solutions (x, y) to the equation= 0 for each integer n (≥ 1). This is again reduced to the problem of determining rational points on curves, which is difficult. However, in 2023, Bell, Matsuzawa, and Satriano proved that for any rational function f of degree 2 or higher, there are no rational pairs (x, y) satisfying f ^n–1(x) ≠ f ^n–1(y) and f ⁿ(x) = f ⁿ(y) for sufficiently large n [9]. In joint work with Matsuzawa, I have generalized this result to two dimensions [10], and Zhong obtained results for higher dimensions [11]. Although these results are about determining rational points on curves, their proofs use algebraic geometry and p-adic analysis.

Fig. 1. Preperiodic orbit.

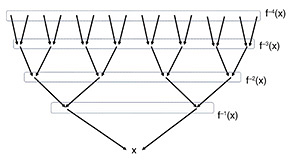
In a different direction from this generalization to higher dimensions, another interesting question is whether the bound on n in dynamical cancellation is independent of f when the degree d is fixed. If this uniform version of dynamical cancellation holds, by considering examples such as those mentioned at the beginning of this section, we can determine the maximum length of the tail of preperiodic orbits, contributing to the Morton–Silverman conjecture.

4. Preimages of 0

Returning to the topic of elliptic curves, let us consider the problem of finding torsion points that become O under repeated multiplication by a prime p. How many such torsion points exist? If it can be shown that there are no such points other than O for all but finitely many p, it would yield a result comparable to Mazur’s theorem. Similar considerations are applied to Abelian varieties. In the context of dynamical systems, consider the analogous problem for the map f_c(z) = z² + c. How many pairs of rational numbers (c, z) and positive integers n satisfy f_cⁿ(z) = 0? This is the problem of determining rational points on the curve X_n^pre defined by f_cⁿ(z) = 0. Faber, Hutz, and Stoll have shown, assuming the BSD conjecture, that for n ≥ 4, there are no rational points (c, z) with c ≠ –1, 0. The map sending a point (z, c) on X_n^pre to (f_c(z), c) on X_n-1^predeeply connects these curves, resembling the modular curves describing torsion points on elliptic curves.

5. Arboreal Galois representations

Shifting direction from the problem of determining rational points on curves, let us consider problems related to extensions of number fields. As in Kummer’s approach to Fermat’s Last Theorem, the uniqueness of prime factorization becomes a crucial issue when extending the world of numbers (i.e., considering number fields). The extent to which unique factorization fails is described by the quantity called the class number. Computing the class number of a given number field remains a central, challenge in modern number theory. For example, Iwasawa’s theory studying the field extension called -extension is one of the great theories in this direction.

In arithmetic dynamics, a similar problem to Iwasawa’s theory arises. Fix an f and rational number x, and consider the tree of points formed by the preimages under iterated composition of f (Fig. 2). The problem of determining the number of rational points in this tree was discussed in section 4, where it was noted that rational points typically disappear early. The field obtained by adding these points to the field of rational numbers is called an iterated Galois extension. How does this extension change as the number of iterations increases? Consider the preimages of 1 under f(z) = z^p. This corresponds to considering all p-th roots of unity. Adding these to the field of rational numbers yields a cyclotomic -extension. When this extension is stopped at the n-th stage, a number field is obtained. In Iwasawa’s theory, the Iwasawa class number formula describes the asymptotic behavior of the class number, which is a remarkable theorem. What about the iterated Galois extensions arising from the preimages of 0 under z² + 1? Is there an asymptotic formula for the class number like Iwasawa’s class number formula? In Iwasawa’s theory, class field theory is used as a fundamental tool, and the commutativity of the Galois group (describing the symmetries of number fields) is an essential assumption. In most cases, however, the Galois group of iterated Galois extensions is non-Abelian and is expected to realize a large part of the symmetry of the tree (the automorphism group). In -extensions, they realize very little of the symmetry of the tree, which is a rare situation. When the Galois group realizes very little of the tree’s symmetry (i.e., when it has an infinite index in the automorphism group of the tree), it is considered that f has special dynamical properties. For example, if the dynamical system has an automorphism, all critical points are pre-periodic points, or the orbits of multiple critical points intersect, the Galois group has an infinite index. However, it is an open question whether these situations exhaust all possibilities for an infinite index. Solving these problems would contribute to the non-Abelian generalization of Iwasawa’s theory.

Fig. 2. Preimage tree.

6. Conclusion

I have introduced several number-theoretic problems arising from the iteration of polynomials and rational functions. These problems not only follow the analogy with the theory of elliptic curves and Iwasawa’s theory but also extend techniques from complex dynamics and reveal new arithmetic phenomena. Arithmetic dynamics is still a young field but developing rapidly, involving researchers from various fields such as algebraic geometry, complex dynamics, and arithmetic geometry. I look forward to future research developments.

References

[1]	R. Irokawa, “How Number Theory Elucidates the Mysteries of Complex Dynamics—Viewed through Non-Archimedean Dynamics,” NTT Technical Review, Vol. 22, No. 9, pp. 30–38, Sept. 2024. https://ntt-review.jp/archive/ntttechnical.php?contents=ntr202409fa3.html
[2]	B. Mazur, “Modular Curves and the Eisenstein Ideal,” Publications Mathématiques de l’IHÉS., Vol. 47, pp. 33–186, 1977. https://doi.org/10.1007/BF02684339
[3]	P. Morton, “Arithmetic Properties of Periodic Points of Quadratic Maps, II,” Acta Arithmetica, Vol. 87, No. 2, pp. 89–102, 1998.
[4]	E. V. Flynn, B. Poonen, and E. F. Schaefer, “Cycles of Quadratic Polynomials and Rational Points on a Genus-2 Curve,” Duke Math. J., Vol. 90, No. 3, pp. 435–463, 1997. https://doi.org/10.1215/S0012-7094-97-09011-6
[5]	S. Michael, “Rational 6-Cycles Under Iteration of Quadratic Polynomials,” LMS Journal of Computation and Mathematics, Vol. 11, pp. 367–380, 2008. https://doi.org/10.1112/S1461157000000644
[6]	A. Wiles, “Modular Elliptic Curves and Fermat’s Last Theorem,” Annals of Mathematics, Vol. 141, No. 3, pp. 443–551, 1995.
[7]	A. Wiles, “Modular Forms, Elliptic Curves, and Fermat’s Last Theorem,” Proc. of the International Congress of Mathematicians, Zürich, Switzerland, 1994, pp. 243–245, Birkhäuser Verlag, Basel, 1995. https://doi.org/10.1007/978-3-0348-9078-6_18
[8]	N. Fakhruddin, “Questions on Self Maps of Algebraic Varieties,” J. Ramanujan Math. Soc., Vol. 18, No. 2, pp. 109–122, 2003.
[9]	J. P. Bell, Y. Matsuzawa, and M. Satriano, “On Dynamical Cancellation,” International Mathematics Research Notices, Vol. 2023, No. 8, pp. 7099–7139, 2023. https://doi.org/10.1093/imrn/rnac058
[10]	Y. Matsuzawa and K. Sano, “On Preimages Question,” preprint, arXiv:2311.02906.
[11]	X. Zhong, “Preimages Question for Surjective Endomorphisms on ” preprint, arXiv: 2311.04349.