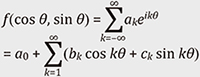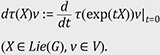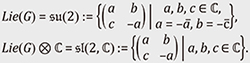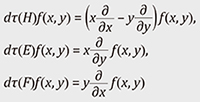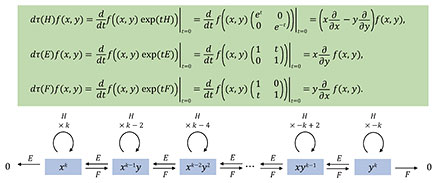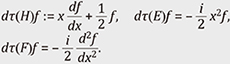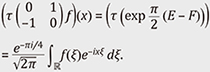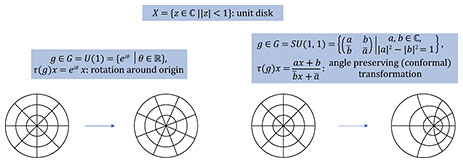
Symmetry and Representation Theory of Lie Groups and Lie Algebras

1. Introduction

Lie groups are abstractions of continuous symmetries of spaces, and linear symmetries are abstracted by representations of Lie groups [1]. These are useful for analyzing functions on spaces with symmetries. However, Lie groups are non-linear objects, and it is not easy to treat their representations directly. To overcome this non-linearity, it is useful to consider the representations of Lie algebras by taking the differentials (linear approximations) of representations of Lie groups. These differentials preserve much information on the original representations and are easier to treat.

2. Representations of Lie groups

First, a Lie group is defined as a subset of the set of all n × n invertible matrices with complex entries (which is denoted as GL(n, ℂ) and called the general linear group), closed by the products, the inverses, and taking the limits^*1. For example, GL(n, ℂ),

are typical examples of Lie groups (where I_n is the identity matrix). Next, let G be a Lie group, and X be a space such that “convergence can be defined” (i.e., a topological space). If a transformation τ(g): X → X is given for each element g ∈ G and if it satisfies the associative law and the continuity in a suitable sense, we say that G acts on X. For example, rotations of the unit disk (the disk of radius 1) around the origin are regarded as the action of the Lie group U(1). Similarly, conformal transformations of the unit disk, i.e., transformations that preserve angles of two intersecting curves, are almost regarded as the action of the Lie group SU(1, 1) (Fig. 1). These examples show that an action of G on X controls the symmetries of X.

Fig. 1. Actions of U(1), SU(1, 1) on unit disk.

When the space X = V on which G acts is a linear space and τ(g) is a linear map on V (i.e., it preserves additions and scalar multiplications), (τ, V) is called a representation of G. For example, if G acts on X, then G acts automatically on the space of functions on X (e.g., V = L²(X) = {ƒ: X → ℂ | ∫_X|ƒ(x)|²dx < ∞}: the space of square integrable functions). This action on L²(X) is linear and becomes a representation of G. Such representation is in general infinite-dimensional and looks difficult, but in many cases, it consists of a sum of simpler representations. Therefore, to understand function spaces, it is important to understand simpler representations in detail.

The most elementary example of representations of a Lie group G ⊂ GL(n, ℂ) is V := ℂⁿ (the space of column vectors), with τ(g) defined by the product of matrices

for each g ∈ G. As more non-trivial examples, for a non-negative integer k, the action of the Lie group G = U(n) on the linear space

(the space of homogeneous polynomials of n variables, degree k), with τ(g) defined by the product of matrices on the variables becomes a representation. Similarly, the action of the Lie group G = O(n) on the linear space

(the space of homogeneous harmonic polynomials of n variables, degree k), with τ(g) defined similarly also becomes a representation. The representation of U(n) on 𝒫_k(ℂⁿ) and that of O(n) on ℋ_k(ℂⁿ) are examples of irreducible representations. “Irreducible” means that the representation can no longer be decomposed, or there are no linear subspaces W ⊂ V satisfying τ(G)W ⊂ W other than {0} and V.

3. Irreducible decompositions of representations—Generalization of Fourier analysis

One of the most fundamental problems in representation theory is to decompose a given representation into a sum of irreducible representations. The irreducible decomposition of the function space (e.g. L²(X)) on X with an action of G is useful for understanding X. For example, G = O(n) acts on the n–1-dimensional sphere S^n–1 := {x ∈ ℝⁿ | ∑ⁿ_i=1x_i² = 1} by the usual rotations and acts on the function space L²(S^n–1) linearly. The space of the restriction of homogeneous harmonic polynomials of degree k on the sphere S^n–1 (spherical harmonic functions, denoted as ℋ_k(ℂⁿ)|_S^n–1 =: ℋ_k(S^n–1)) is then preserved by this action, and becomes a sub-representation. Namely,

Moreover, each ƒ(x) ∈ L²(S^n–1) is expressed uniquely by the form

Hence, L²(S^n–1) is decomposed into the direct sum

Since each ℋ_k(S^n–1) is irreducible, this gives the irreducible decomposition. When n = 2, by the coordinate (cos θ, sin θ) of S¹, we have

and the above decomposition coincides with the Fourier series expansion

(b_k = a_k + a_–k, c_k = i(a_k – a_–k)). Similarly, the (inverse) Fourier transform

is regarded as the decomposition of the function space L²(ℝ) on the real line ℝ into the sum of one-dimensional sub-representations ℂe^ixξ as the representation of the additive group ℝ,

Note that this is a sum of uncountably many spaces and called the direct integral instead of the direct sum. Needless to say, the Fourier analysis is important in many fields such as signal processing, and the theory of spherical harmonics is important in the treatment of rotation-invariant systems in quantum physics. Irreducible decompositions of general representations are regarded as generalizations of these important theories.

Among irreducible decompositions, the decomposition of a representation of G under its subgroup G' ⊂ G is called the branching law. For example, we consider the restriction of the representation 𝒫_k(ℂⁿ) of G = U(n) to the subgroup

Then as a representation of U(n), 𝒫_k(ℂⁿ) is irreducible but as a representation of U(n – 1), the subspaces

(m = 0, …, k) are clearly sub-representations. Therefore, we find that the irreducible decomposition (branching law) of 𝒫_k(ℂⁿ) under U(n – 1) is given by

Similarly, it is known that the irreducible decomposition of 𝒫_k(ℂⁿ) under G' = O(n) is given by

(where ‖x‖² := ). As a more non-trivial example, we consider the branching law of the representation ℋ_k(ℂⁿ) of G = O(n) under the subgroup G' ≃ O(n – 1). For m = 0, 1, …, k, let be a polynomial of degree at most k – m satisfying and we consider the linear space

This is then an irreducible representation of O(n – 1), and if we suitably choose , then we can make W_m ⊂ ℋ_k(ℂⁿ). In this situation, ℋ_k(ℂⁿ) is irreducibly decomposed under O(n – 1) as

The polynomial is obtained by solving a differential equation concerning the Laplacian and given explicitly by using the Gegenbauer polynomial . When n = 3, this is given by a constant multiple of the associated Legendre polynomials. With these polynomials, we can explicitly construct a basis of ℋ_k(ℂⁿ) inductively on n (Fig. 2: n = 3).

Fig. 2. Express ℋ_k(S²) = ℋ_k(ℂ³)|_S² by sum of ℋ_m(S¹) = ℋ_m(ℂ²)|_S¹.

4. Representations of Lie algebras—Linear approximation of those of Lie groups

Lie groups are generally not linear spaces, and it is not easy to treat their representations directly. To overcome this non-linearity, we consider the Lie algebras associated with the Lie groups instead. For X ∈ M(n, ℂ) (an n × n matrix with complex entries) and t ∈ ℝ, we consider the exponential function exp(tX) := This satisfies the usual law of exponents exp((s + t)X) = exp(sX) exp(tX) and exp(tX)|_t=0 = X. By using this, we define the Lie algebra Lie(G) ⊂ M(n, ℂ) associated with the Lie group G ⊂ GL(n, ℂ) by

This then becomes a linear space, and [X, Y] := XY –YX ∈ Lie(G) holds for all X, Y ∈ Lie(G). Next, for a finite-dimensional representation (τ, V) of G, we define the representation (dτ, V) of the Lie algebra Lie(G) by

Then dτ(aX + bY) = adτ(X) + bdτ(Y) and dτ([X, Y]) = dτ(X)dτ(Y) – dτ(Y)dτ(X) hold for all X, Y ∈ Lie(G), a, b ∈ ℝ. This representation (dτ, V) preserves most information on the original representation (τ, V). For example, if G is connected, then the irreducibility of a finite dimensional representation (τ, V) under G is equivalent to the irreducibility of the differential representation (dτ, V) under Lie(G).

Let us consider the representation of G = SU(2) := U(2) ∩ SL(2, ℂ) on V = 𝒫_k(ℂ²) as an example. First, the Lie algebra Lie(G) associated with G = SU(2) and its complexification Lie(G) ⊗ ℂ are given by

We take a basis of (2, ℂ). Then their actions on 𝒫_k(ℂ²) are given by

(see Fig. 3 for the intermediate process). In particular, the actions on the basis {x^k, x^k–1y, x^k–2y², …, y^k} of 𝒫_k(ℂ²) is written as

Hence, dτ(H) has the eigenvalues {k, k – 2, k – 4, …, –k}, dτ(E) raises the eigenvalue of an eigenvector of dτ(H) by 2, and dτ(F) lowers the eigenvalue by 2. This structure is equivalent to those of the spin representations appearing in quantum physics. In fact, a general irreducible representation of SU(2) always has such a structure, especially equivalent to 𝒫_k(ℂ²) for a non-negative integer k. As a higher example, we consider the representations of the Lie group U(n). Again, by looking in detail at the action of (the complexification of) the associated Lie algebra for diagonal, upper-triangular, and lower-triangular matrices, we can then show that the set of all irreducible representations of U(n) has a one-to-one correspondence with the set of n-tuples of decreasing integers

As we have seen above, representations of Lie algebras are helpful for the classification of representations of Lie groups. It is also known that the dimension of each irreducible representation of U(n) is characterized by the number of combinatoric objects called the semistandard Young tableaux.

Fig. 3. Representation of Lie algebra of SU(2) on 𝒫_k(ℂ²).

5. Example of infinite-dimensional representations

Next, we consider an example of infinite-dimensional representations. Let us consider the Lie group G = SL(2, ℝ). Its Lie algebra is then given by

We take the basis H, E, F ∈ (2, ℝ) as before and define the action of (2, ℝ) on (some dense subspace of) V = L²(ℝ) by

This does not lift to a representation of the Lie group SL(2, ℝ) but lifts to that of the double covering group (2, ℝ) (that is, there exists a representation (τ, L²(ℝ)) of (2, ℝ), the differential of which coincides with the above dτ (on some dense subspace)). The action of also coincides with a constant multiple of the Fourier transform.

This is proved by observing the eigenfunctions of (the quantum harmonic oscillator). While the representation (τ, L²(ℝ)) is infinite-dimensional, this is nearly irreducible^*2 and called the Weil representation or the metaplectic representation. This construction is generalized to the representation L²(ℝⁿ) of the larger Lie group Sp(n, ℝ) (Sp(1, ℝ) = SL(2, ℝ) for n = 1 case). By taking the irreducible decomposition of the representation of Sp(nm, ℝ) on L²(ℝ^nm) ≃ L²(M(n, m; ℝ)) (the function space on n × m matrices) under the subgroup Sp(n, ℝ) × O(m) ⊂ Sp(nm, ℝ), we can also obtain various representations of Sp(n, ℝ); thus, this Weil representation is considered quite important in representation theory.

6. Branching law of infinite-dimensional representations

In recent research, I was interested in explicitly determining the branching laws of infinite-dimensional representations (see [2] and references therein). When we restrict a “good” representation (τ, V) of G to a subgroup G' ⊂ G, V is decomposed into a direct sum (or a direct integral) of (in general infinite number of) irreducible representations of G'. Even if we know which representation V' of G' appears abstractly in the decomposition of V, it is generally a difficult problem to determine how V' is included explicitly in V (corresponding to the determination of in the example of ℋ_k(ℂⁿ)). I determined the explicit inclusion map (intertwining operator) from V' into V for “good” tuples (G, G', V, V') [3, 4] (Fig. 4). There then appear special functions such as hypergeometric functions (and their multivariate generalizations). In the future, I aim to obtain analogous results for more general tuples (G, G', V, V').

Fig. 4. Example of my results.

References

[1]	A. W. Knapp, “Lie Groups Beyond an Introduction,” Progr. Math., Vol. 140, Birkhauser Boston, Inc., Boston, MA, USA, 1996.
[2]	T. Kobayashi, “A Program for Branching Problems in the Representation Theory of Real Reductive Groups,” Representations of Reductive Groups, Progr. Math. Vol. 312, pp. 277–322, Birkhäuser/Springer, Cham, 2015. https://doi.org/10.1007/978-3-319-23443-4_10
[3]	R. Nakahama, “Construction of Intertwining Operators between Holomorphic Discrete Series Representations,” Symmetry, Integrability and Geometry: Methods and Applications (SIGMA), Vol. 15, 036, 2019. https://doi.org/10.3842/SIGMA.2019.036
[4]	R. Nakahama, “Computation of Weighted Bergman Inner Products on Bounded Symmetric Domains and Restriction to Subgroups,” SIGMA, Vol. 18, 033, 2022. https://doi.org/10.3842/SIGMA.2022.033