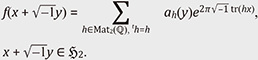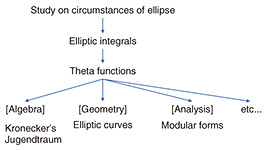
Modular Forms and Fourier Expansion

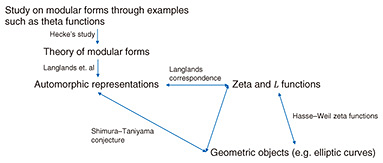
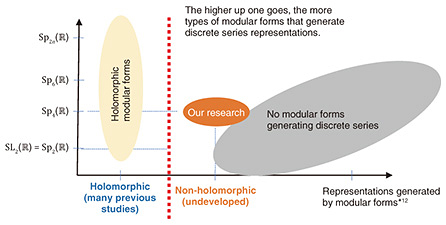
1.1 Developments of the theory of modular forms and obstructions

To further developments in the theory of modular forms, we needed to wait for the study of modular forms of Hecke, a student of Hilbert. Of course, there are many known results for modular forms, but Hecke arranged such results and initiated the theory of modular forms. Hecke defined the zeta functions and L functions for modular forms on the basis of the Riemann zeta function. These results opened the way for the theory of modern modular forms. This theory became the theory of automorphic representations through the works of Langlands and other mathematicians. To review the theory of automorphic representations, the Shimura–Taniyama conjecture is one of the most significant results. It is a profound conjecture that connects automorphic representations and elliptic curves. In 1995, Wiles solved the “semistable” case of the conjecture, proving Fermat’s conjecture completely. The Shimura–Taniyama conjecture has now been completely proven. The paramodular conjecture, a generalization of the Shimura–Taniyama conjecture, has been partially proved. To formulate these conjectures, it is necessary to use automorphic representations, which also play a vital role in these conjectures.

We stated that the Shimura–Taniyama conjecture connects geometric objects, such as elliptic curves, and analytic objects such as holomorphic modular forms. Through the pioneering studies of many researchers, for example, Shimura and Langlands, the Shimura–Taniyama conjecture exceeds the original formulation and became a theory to unify algebra, analysis, and geometry (Fig. 2). However, there is a remaining problem in the theory of modular forms, i.e., a study of non-holomorphic modular forms. Shimura and Taniyama formulated the conjecture on the basis of many numerical computations of Fourier coefficients of modular forms. However, no known examples of Fourier coefficients of non-holomorphic modular forms exist. The lack of such examples is an obstruction of further development. Recall that we prove the Shimura–Taniyama conjecture and hypersphere packing problem^*3 using holomorphic modular forms. It is easy to imagine that non-holomorphic modular forms have several applications similar to holomorphic modular forms, but there is room for improvement in modular forms. In this article, we first discuss the relationship between Fourier expansion and representation theory then discuss the Langlands conjecture and Arthur conjecture, which may be viewed as a generalization of the relationship, and introduce a joint study with myself and Narita, a professor of Waseda University, about Fourier expansion of non-holomorphic modular forms.

Fig. 2. Modular forms, zeta and L functions, geometric objects.

2.1 Fourier expansion

Many people may have heard of Fourier expansion and Fourier transform. These are indispensable techniques for modern society; for example, they are frequently used to process sound signals. No matter how complicated sounds are, we may construct complex sounds using simple ones such as the time signals on television and radio. This point of view is the method of Fourier transform and Fourier expansion. In mathematics, one may regard such simple sounds as sin x and cos x functions. In pure mathematics, Fourier expansion means an expansion of periodic functions as sin x and cos x, and Fourier coefficients are the coefficients in such an expansion. Fourier expansion plays a significant technical and theoretical role in modern mathematics. We first discuss the relationship between Fourier analysis and representation theory.

The philosophy of Fourier expansion and Fourier transform is to understand the space of periodic functions via the translations for periodic functions. To understand this, we discuss the mathematical details. Let ƒ be a complex-valued function on the space of real numbers ℝ. We say that ƒ has the period 1 if ƒ(x + 1) = ƒ(x) for any x ∈ ℝ. Thus, we may regard ƒ as a function on ℝ/ℤ. The theory of Fourier expansion tells us to rewrite ƒ as a sum of sin x and cos x. More precisely, by = cos(2𝜋nx) + sin(2𝜋nx), we have an infinite sum

Such an expression is called Fourier expansion, and coefficients a_n are the Fourier coefficients. It is known that a_n equal Fƒ(n), where Fƒ is the Fourier transform.

In representation theory, we divide mathematical objects, such as periodic functions, into smaller objects with more precise conditions such as periodic functions. A typical example of representation theory is the action of matrices on vector spaces. We can easily understand the action of matrices by dividing them into eigenvalues and eigenvectors. Such a framework is one fundamental aspect of representation theory.

Next, we discuss the relationship between Fourier analysis and representation theory. In the above representation theoretical method, we consider the vector spaces and the matrices acting on them as the space of periodic functions and the “translation,” respectively. For a periodic function ƒ and real number y ∈ ℝ, we define the translation r_y by r_yƒ(x) = ƒ(x + y). Then, the n-th Fourier coefficient of r_yƒ equals a_n. Therefore, the action defined by the translation r_y by y has the function x ↦ as an eigenfunction and as the eigenvalue of it. Summarizing thus far, by combining the period function, Fourier transform, and the translation, we conclude that the following two objects relate:

• Representations on ℝ/ℤ defined by y ↦
• n-th term of Fourier expansion of period functions

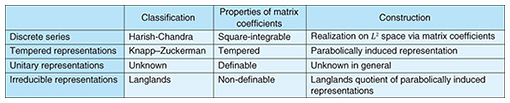
We thus grasp one face of representation theory by connecting a function and representations, a mysterious object. We may find this a surprising correspondence in a broad framework rather than an easy object ℝ/ℤ. The central theme of the next section is a generalization of such surprising correspondence.

2.2 From Fourier analysis to Langlands conjecture

We deeply observe the relationship between functions and representations for ℝ/ℤ and period functions. A fundamental property is the “compactness” of ℝ/ℤ. For a non-compact object such as the real numbers ℝ, such correspondence becomes more difficult due to technical difficulties, for example, a convergence of integrals. We may find differences between Fourier analysis of period functions and a function on ℝ in certain literature on Fourier analysis. The nature of these differences comes from the topological property of ℝ and ℝ/ℤ, i.e., the non-compactness of ℝ.

Harish-Chandra produced a breakthrough in the representation theory of reductive groups, one of the most essential classes of non-compact groups. He mainly considered the Lie groups, containing ℝ and ℝ/ℤ. His pioneering work is the classification of discrete series representations. Recall that we consider the space of functions for ℝ and ℝ/ℤ. For reductive groups G, he considered the space L²(G) of square-integrable functions^*4 and translations on it. We may naturally find discrete series representations in L²(G). A realization of discrete series representations on L²(G) is done by matrix coefficients^*5. Like this, we highly develop the representation theory through a space of certain functions and analysis. On the basis of Harish-Chandra’s study, Knapp and Zuckerman classified the tempered representations, and Langlands classified all the irreducible representations of Lie groups (Table 1). This classification is due to Langlands and is called the Langlands classification. Since Lie groups are a theory for ℝ or complex numbers ℂ, number theorists need a similar theory for p-adic groups.

Table 1. Classification and construction of representations.

On the basis of various trials and errors, the local Langlands conjecture, the classification theory of irreducible representations on p-adic groups, was becoming clear. The local Langlands conjecture states the correspondence of the following two objects for a connected reductive group G^*6:

L parameters on the right side are arithmetic objects and define an L function.

As in another article [1] in this issue, one aspect of the local Langlands conjecture is a non-commutative class field theory. Such an aspect appears in the L parameters. The local Langlands conjecture has made significant progress and become more precise. It is now called the endoscopic classification.

The representation theory of p-adic groups and modular forms or automorphic representations are inseparable. They have a history of developing together while compensating for each other’s weaknesses. Finally, we discuss the author’s results for the Fourier expansion of non-holomorphic modular forms.

3.1 Fourier expansion of holomorphic modular forms

We first consider the Fourier expansion and coefficients of holomorphic modular forms. Let be the upper half plane^*7 and SL₂(ℝ) be the special linear group of degree two^*8. The group SL₂(ℝ) acts on by the linear fractional transformation^*9. Let Γ = SL₂(ℤ) be the subgroup of SL₂(ℝ) with integer entries. Set j to be the factor of automorphy^*10. Take an integer k and holomorphic function ƒ on . We say that ƒ is a modular form^*11 of weight k with respect to Γ if for any z ∈ and γ ∈ Γ. Thus, modular forms are not entirely invariant under Γ other than k = 0 but is invariant under Γ with certain modified factors due to k and j. In particular, one would obtain ƒ(z + 1) = ƒ(z) for a modular form ƒ. Since ƒ is holomorphic, one obtains the following Fourier expansion by Cauchy’s integral formula:

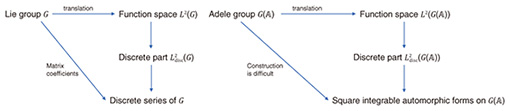
Surprisingly, a_n are independent of the imaginary part y under this expression. This expression is usually called the Fourier expansion of ƒ, and a_n are called the Fourier coefficients of ƒ.

3.2 Modular forms and representation theory

We observed a strong relationship between translations on function spaces and representation theory. Similar phenomena may occur for modular forms. More precisely, we may lift modular forms to functions on a Lie group. Let φ_ƒ be the lift of ƒ. We then may regard φ_ƒ as a function on C^∞(Γ∖SL₂(ℝ)). As we have seen in the section discussing the Fourier expansion, one can define the right translation by SL₂(ℝ) on the space Γ∖SL₂(ℝ). Thus, modular forms and representation theory of SL₂(ℝ) relate. With a similar method, modular forms would become a function φ_ƒ on an adele group SL₂(𝔸) using the adele ring 𝔸 of ℚ. If ƒ is square-integrable or more strongly ƒ is a cusp form, φ_ƒ is a function on L²(SL₂(ℚ)∖SL₂(𝔸)). We summarize that from a square-integrable modular form ƒ, the function φ_ƒ becomes a function on L²(SL₂(ℚ)∖SL₂(𝔸)) and relates representations of SL₂(ℝ) and SL₂(ℚ_p). This phenomenon resembles Fourier analysis and representation theory (Fig. 3).

Fig. 3. Comparison of local and global.

In the modern modular form theory, we generalize SL₂ in L²(SL₂(ℚ)∖SL₂(𝔸)) to a connected reductive group. Like Harish-Chandra’s study on discrete series, we may consider the discrete spectrum of L²(SL₂(ℚ)∖SL₂(𝔸)). A recent study gives us a description of such a discrete spectrum. This study is based on the research of many researchers. Arthur, a student of Langlands, established the Arthur conjecture, which describes the discrete spectrum and proves his conjecture for orthogonal and symplectic groups under appropriate modification. This study is one of the highest peaks in modern theory of modular forms. Many researchers now consider generalizations and applications of Arthur’s study.

3.3 Toward the generalization of Fourier expansion of modular forms

We saw that the Fourier coefficients of holomorphic modular forms ƒ are constant. This fact is based on the holomorphy of ƒ. Thus, if we remove the holomorphy assumption, the Fourier expansion of ƒ is expressed as

The coefficients a_n(y) depend on the imaginary part y. Therefore, it is not easy to consider a_n(y). In the joint study with Narita [2], we treat such Fourier expansion of non-holomorphic modular forms. A typical example of a non-holomorphic modular form is a Maass form, but we do not treat Maass forms. Our main target is a modular form naturally arising from representation theory^*12. Discrete series representations are a key idea in our joint study. We recall Harish-Chandra’s classification of discrete series representations to understand the idea. The modular form on the upper half plane corresponds to a function on SL₂(ℝ). In a certain sense, there is essentially only one discrete series representation of SL₂(ℝ). One of the difficulties of Maass form is that the corresponding representation is not a discrete series representation. An example of a group with non-holomorphic discrete series representations is the symplectic group Sp₄(ℝ) of degree two. For Sp₄(ℝ), there are essentially two discrete series representations in a certain sense. One is holomorphic and the other one is non-holomorphic. Also, Sp₄(ℝ) is a minimal with such a property. We may define a modular form on Sp₄(ℝ). Such a modular form is a function on the Siegel upper half plane of degree two^*13 satisfying the Fourier expansion:

The a_h(y) are called the generalized Whittaker function. Unlike holomorphic modular forms, a_h(y) are never a constant. We can introduce a differential equation to evaluate a_h(y) when considering the discrete series representations. In our joint study, we explicitly compute the solution of the differential equation and prove several properties of a_h(y). As an application, we explicitly describe the space of all the non-cuspidal automorphic forms, generating discrete series representations of Sp₄(ℝ). As in Fig. 4, this joint study is the first to describe all the non-cuspidal modular forms, including their construction. In our next joint study, we will consider an explicit computation of Fourier coefficients. We will extend our research to provide an arithmetic property of L function through explicit computation of modular forms corresponding to discrete series representations.

Fig. 4. Current status of mine and Narita’s.