|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
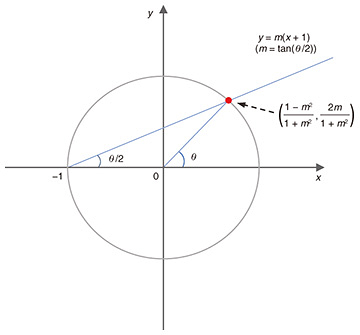
Feature Articles: Challenging the Unknown: Mathematical Research and Its Dreams Vol. 22, No. 9, pp. 16–25, Sept. 2024. https://doi.org/10.53829/ntr202409fa1 A Mathematical World Woven by Number Theory, Algebraic Geometry, and Representation TheoryAbstractThrough basic research in mathematics, the NTT Institute for Fundamental Mathematics aims to enrich the “fountain of knowledge” that nourishes science and technology. In this article, we first provide an overview of the research being carried out at the Institute then introduce the Institute’s core research areas: number theory, especially arithmetic dynamics; algebraic and arithmetic geometry; and representation theory and automorphic forms. Keywords: elliptic curve, Galois theory, zeta function 1. A mathematical world woven by number theory, algebraic geometry, and representation theoryIt is quite impressive that research into prime numbers was being carried out in Greece approximately 2500 years ago. Two early important achievements were the proofs of the infinitude of prime numbers (in a constructive way), and the unique factorization of natural numbers into products of prime numbers. The original motivations for this research remain unclear. Until the invention of the RSA public-key cryptosystem by Rivest, Shamir, and Adelman in 1977, there was no expectation for applications of number theory to engineering or society. In fact, it took more than 300 years to establish RSA since the discovery of Fermat’s little theorem [1] (proved by Leibniz): “if p is a prime number and a is an integer, then ap ≡ a (mod p) holds,” which is one of the key technical results needed for public-key cryptosystems. Number theory is the branch of mathematics that studies the properties of numbers, especially integers and number systems and structure derived from them [2]. These systems include algebraic number fields such as the rational number field, made up of all fractions with the four basic operations (addition, subtraction, multiplication, and division); finite fields; local fields, such as the real number field; the set of numbers obtained as limits of sequences of rational numbers; and the fields of p-adic numbers. Number theory is said to have originated in the study of Diophantine equations during the Roman Empire. Diophantine equations are defined using polynomials with rational coefficients. Although it was desirable to completely solve them, this is generally difficult. Therefore, the interest was directed toward solutions that are rational numbers. This is probably because irrational numbers were thought to be incomplete numbers, being defined as limits of rational numbers. Although there is an infinite number of rational numbers, most real numbers are in fact irrational. Lumping them together would be like ignoring the dark matter in the universe. It would be unsatisfactory as science. For example, the equation x2 – 2 = 0 has an irrational solution, √2. Irrational numbers, such as √2 and 3√3, are called algebraic numbers and distinguished from transcendental numbers such as 𝜋, Napier’s number e, and 2√2. For √2 and 3√3, it is possible to compute √2 × 3√3 = 6√72 without going back to their definition as limits of rational numbers. In other words, the set of algebraic numbers defines a closed system of numbers within itself. Other types of numbers, such as √–1, have also been introduced and has enabled the expansion of the concept of numbers. Even today, mathematicians are conscious of the problem of finding new classes of numbers that are broader than algebraic numbers. There is hope that we can find a broad, algebraically controlled class of transcendental numbers that have integral expressions called “periods,” such as pi, 𝜋 = ∫x2+y2<1 dxdy. This is known as the Kontsevich–Zagier conjecture. Although it seems difficult to solve the conjecture affirmatively, it is a sort of ideal guiding research. These attitudes toward numbers are also closely related philosophically to the three major classic Greek drawing problems of doubling the cube, angle trisection, and squaring a circle, which were proven unsolvable. To determine whether a given equation has a rational solution is a very delicate issue. For instance, the equation x2 + y2 = 1 (unit circle) has an infinite number of rational points, that is, with coordinates given by rational numbers. It is easy to confirm this by considering the intersection of a circle with a straight line that passes through the point (–1,0) and has a slope of tan θ/2 on a plane (using the double angle formula for trigonometric functions) (Fig. 1). However, there are no rational points on the circle x2 + y2 = 0.999999, which is a slightly shrunk version of the unit circle. Speaking of subtleties, it took about 350 years to solve Fermat’s conjecture (Last Theorem), which states that there are no rational points other than the obvious ones on xn + yn = 1 (n=3,4,5...). This could not have been achieved without rich theories that make full use of the best of modern mathematics to go beyond a pure algebraic perspective and transcend the circle (which has the structure of an abelian group with addition as a product operation according to the addition theorem) to recognize the agreement between the zeta function determined locally from a geometric structure of an abelian group called an elliptic curve (Fig. 2) and a zeta function defined globally and related to representation theory.
The statement of problems in number theory, including the Fermat conjecture, are usually easier to understand than problems in other fields of mathematics. The same can be said for combinatorics and graph theory. Some of the problems in combinatorics and graph theory, such as the construction of Ramanujan graphs, are deeply related to number theory and representation theory, and play a prominent role in applications, including the construction of efficient networks. To solve these problems, a wide variety of methods are used, including using highly advanced modern mathematical tools (rather than just formulas and equations, they use abstract concepts and techniques, e.g., considering the relations of objects with “arrows →”). For this reason, many conjectures (statements with supporting evidence but without mathematical proof) that appear sometimes simple remain unsolved. Two of the most well-known and challenging mathematical problems (both in number theory) are the Riemann Hypothesis, which has remained inaccessible for 165 years since its conception, and the Birch and Swinerton-Dyer (BSD) conjecture, which describes the set of rational solutions defining an elliptic curve. The Ramanujan and Weil conjectures, which were solved by Deligne thanks to Grothendieck’s innovations in algebraic geometry, led number theory research in the 20th century. The Taniyama–Shimura conjecture, which was the key to the Fermat conjecture, and the Langlands program, which aims to construct a non-commutative class field theory, give us grand dreams for the future. What is particularly noteworthy is that many of these can be expressed as the correspondence of zeta functions and L-functions with different origins, including class field theory. There is also active research into deriving number-theoretic properties from abstract geometric objects, e.g., investigating rational points and integer points on orbits under dynamical systems determined by repeated composition of polynomials and rational functions and regarding finite-order points on figures with an abelian group structure as periodic points. For example, the far-unexplored Vojta conjecture in Diophantine geometry, which includes the Mordell conjecture (Faltings’ theorem), may be understood from this perspective. It is thus not an exaggeration to say that number theory is voracious. It will use anything, including geometry, analysis, and probability theory, if necessary to solve a problem. It actively draws on geometric inspiration to derive number-theoretic properties from the geometric properties of abstract figures, it makes extensive use of functions that precisely incorporate infinity while retaining invariance, and even incorporates measure theory into its scope of discussion by closely observing distributions and density patterns that are familiar in probability theory. Therefore, it does involve many fields of mathematics to advance its research but contributes to the development of each of them. Bernhard Riemann’s research into analytic number theory, which began with the distribution of prime numbers, promoted the development of the theory of complex functions with one variable. It was Carl Friedrich Gauss, the greatest mathematician of the 19th century, who said, “Mathematics is the queen of science, and number theory is the queen of mathematics.” This is usually taken to be a succinct expression of the beauty of number theory, but the true meaning may be about the brilliant use of a variety of mathematics to actualize this beauty. The mathematical research covered in the Feature Articles in this issue [3–9] has as its background theories of arithmetic geometry, which explores problems in number theory using methods from algebraic geometry, arithmetic dynamics, dynamical systems of complex and p-adic fields, and automorphic forms, as well as representation theory. Representation theory is directly or indirectly related to number theory, mathematical physics, combinatorics and graph theory, special function theory, and differential equations and topology. For this reason, the NTT Institute for Fundamental Mathematics, to which the authors belong, is an organization that promotes research that is both cohesive and expansive in the field of mathematics, not only because of its appetite for number theory but also because of the central role of representation theory, a field that deals with symmetry and is at the intersection of algebra, geometry, analysis, and probability theory and has a wide range of applications. We have put together these articles in the hope that readers will be provided a glimpse into some of the major trends in modern mathematics. 2. Number theory and arithmetic dynamics2.1 Fermat’s Last TheoremPierre de Fermat wrote “Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.” (I have discovered a truly marvelous proof of this theorem, which however the margin is too small to contain.) in the margin of his copy of Diophantus’ “Arithmetica.” After the annotated edition of “Arithmetica,” in which the problem he noted was published in 1670, many mathematicians challenged it for over 300 years until Andrew Wiles finally proved it in 1995. This theorem laid the foundation for the development of arithmetic geometry. Fermat’s Last Theorem: For any integer n greater than 2, there are no rational pairs (x, y) satisfying the equation (1) xn + yn = 1 with x, y ≠ 0. When n = 2, the equation defines a circle with radius 1 centered at the origin. This circle has infinitely many rational points (= points with rational coordinates). All these rational points can be represented as intersections of the circle with lines having rational slopes passing through (–1, 0). This means the rational points on the curve can be parameterized by a single parameter t, the slope of the line. The space of all such slopes is called the projective line. If we extend the coordinates to complex numbers, the figure defined by (1) becomes a real surface. The number of holes in this surface is called the genus. Geometrically, the projective line is a smooth curve of genus 0, while a smooth curve of genus 1 is known as an elliptic curve. Over complex numbers, an elliptic curve looks like a torus (Fig. 3).
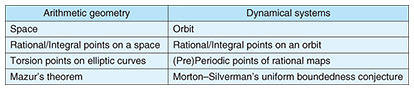
For n = 3 and n = 4, the curves defined by (1) are elliptic curves. Fermat proved the theorem for n = 4 using a method called infinite descent, which was later extended to the proof of Mordell–Weil theorem. For n = 3, the proof was achieved by extending the world of numbers from rational numbers to numbers including the cubic root of unity and using the uniqueness of prime factorization in this larger number system. Today, this involves considering extensions of a number field. Although unique factorization does not hold in general number fields, Kummer’s theory of ideal numbers, developed to overcome this, became today’s ideal theory. The concept of field extensions laid the foundation for Galois theory and is crucial in modern number theory and arithmetic geometry. For m ≥ 5, the curve defined by (1) is of genus greater than or equal to 2, and Mordell’s conjecture (Faltings’ theorem) implies that such a curve has only finitely many rational solutions. Mordell’s conjecture (Faltings’ theorem): A smooth curve defined by polynomials with rational coefficients has only finitely many rational points if its genus is 2 or more. This theorem is a remarkable connection between geometric information (the genus of the curve) and an arithmetic phenomenon (the finiteness of rational points). This result earned Faltings the Fields Medal in 1986. Although there is much more history to be discussed regarding Fermat’s Last Theorem, we conclude this section. 2.2 Elliptic curvesWe mentioned that smooth curves of genus 0 can be parameterized by rational points, but it is not as simple for genus 1 elliptic curves. However, elliptic curves allow an “addition” where rational points can be added together to produce new rational points. This means the set of rational points on an elliptic curve forms a group. This operation enables us to create new rational points from known rational points. One of the key results is the Mordell–Weil theorem. Mordell–Weil theorem: There exist finitely many rational points P1, P2, …, Pr, Q1, Q2, …, Qs on an elliptic curve E such that any rational point P on E can be uniquely expressed as P = n1P1 + n2P2 + … + nrPr + Qt (n1, n2, …, nr are integers, 1 ≤ t ≤ s), where Q1, Q2, …, Qs are points that become O (the identity element, i.e., P + O = P for any rational point P) under multiplication by some positive integer. The number r is called the rank of the elliptic curve E, and Q1, Q2, …, Qs are called the torsion points of E. While Mazur has completely analyzed the group structure when restricted to torsion points, there remain many unresolved issues concerning the rank. One of the Millennium Prize Problems is the BSD conjecture, which examines the coincidence between the rank and order of the zero of the L-function. The existence or non-existence of elliptic curves with arbitrarily large ranks also remains an open problem. The current world record for the highest known rank, achieved by Elkies, is at least 28. It may be surprising at how small this record is, given the question of whether it is infinite. 2.3 Arithmetic dynamicsProblems in the field of arithmetic dynamics can be traced back to Northcott’s theorem in 1950, which states that a morphism defined over a number field on projective space has only finitely many rational periodic points. However, the term “arithmetic dynamics” started being used from 2000. It was clearly recognized as one field of study when the 2010 Mathematics Subject Classification (MSC2010) included 11S82 Non-Archimedean dynamical systems and 37Pxx Arithmetic and non-Archimedean dynamical systems. Broadly speaking, arithmetic dynamics studies the behavior of rational points under the iteration of polynomials or rational maps defined over fields of arithmetic interest (such as p-adic fields or the field of rational numbers). Depending on whether the emphasis is more on number theory or dynamical systems, the nature of the research varies. From a number-theoretic perspective, a large goal might be to create a dictionary of analogies (or generalizations) between results about abelian varieties in number theory and their dynamical system analogs or to obtain new insights into arithmetic geometry through these analogies. Although detailed terminology cannot be explained due to space limitations, the following analogies are being considered (Table 1).
Problems regarding arithmetic dynamics over number fields are detailed in the article “Arithmetic Problems in Dynamical Systems” in this issue [3]. When the emphasis is placed on dynamical systems, the field appears somewhat more descriptive. There is an effort to trace similarities between non-Archimedean dynamical systems (such as those on p-adic fields) and complex dynamical systems, with applications to both complex dynamics and arithmetic dynamics. These topics are introduced in the article “How Number Theory Elucidates the Mysteries of Complex Dynamics—Viewed through Non-Archimedean Dynamics” in this issue [4] (Fig. 4). Many books and surveys on arithmetic dynamics have been published, and extensive bibliographies [10] have been compiled. Simply glancing at the titles of the papers listed in these bibliographies reveals the rapid growth of this new field.
3. Algebraic geometry and arithmetic geometry3.1 A bridge between algebra and geometrySolving equations is a fundamental but difficult task in mathematics. One of the ultimate goals in the field of algebra is to understand the behaviors of all equations of the form “polynomial(s) = 0,” called algebraic equations. Taking their “graphs” is a very important technique when studying algebraic equations. The graphs are “shapes,” for example, the graph of the algebraic equation x2 + y2 = 1 is nothing but the circle with radius 1 centered at the origin. The graph of y = m(x + 1) is the straight line with slope m passing through the point (–1, 0). The common solutions of the two equations are also expressed as the intersection of the two graphs (Fig. 1). Therefore, graphs transform algebraic problems into geometric ones, enabling us to benefit from the very rich intuition, tools, and ideas from geometry. The method of graphs was established by René Descartes in his book “Discours de la méthode” published in 1637, and it is now taught in primary education worldwide. However, there are limits to the intuitive method. If we increase the number of variables in the equations, their graphs are (usually) not able to be embedded into the three-dimensional spaces where we live; hence, we cannot “see” the graphs directly. Even if the graphs are (luckily) embedded in the three-dimensional space, their shapes could be too complicated to study just by seeing them with our eyes. After Descartes, many mathematicians made tremendous efforts over the centuries to overcome these difficulties. Finally, we reached the huge theoretical system called “algebraic geometry.” The development of the theory of algebraic geometry throughout the 19th to the 20th centuries was so rapid and innovative, and it had many irreversible effects on mathematics afterwards. 3.2 A mathematical paradigm shift—Which came first, functions or spaces?A breakthrough in mathematics is often accompanied with an important paradigm shift—in the case of algebraic geometry, it came from the relationship between spaces and functions. In modern mathematics, geometric objects are called “spaces.” The graphs of algebraic equations are also spaces. A function is a rule assigning a value to each point on a space. For example, we have a function ƒ(x) = x + 1 on the real number line. The values of a function are just numbers, so we can define the addition, subtraction, and multiplication of functions on a space (we cannot define the division of functions in general since the value of a function could be zero, and the division by zero is not defined). An algebraic structure consisting of addition, subtraction, and multiplication is generally called a “ring.” In the above discussion, we have seen that the set of functions on a space has a natural structure of a ring. Let us consider the formula ƒ(x) = 1/x, which associates to each x its reciprocal. In fact, this does not define a function on the entire real number line. Indeed, x = 0 does not have a reciprocal. However, if we consider the space obtained by removing the origin from the real number line, then ƒ(x) = 1/x defines a function on it. This in turn shows that, if a function ƒ(x) = 1/x lives on a space, the space cannot contain zero. In this way, a space determines the ring of functions, and on the contrary, the structure of the ring of functions reveals the property of the space. This phenomenon can be expressed, metaphorically, as follows: if we regard a space as a kind of a nation, then the functions on the space could be thought of as the people living in the nation. If we have a nation, there are people living there and they are interacting with each other via “+, –, ×.” Conversely, if we want to know about the nation, it would be very effective to see the people there and how they interact. On the basis of this observation, Alexander Grothendieck, one of the greatest mathematicians in the history of modern mathematics, boldly claimed that, “Any ring is the ring of the functions on a space.” In other words, he claimed that starting from any ring (which could be purely algebraic and could have nothing to do with geometry a priori), we can always find a certain space and regard each member of the ring as a function on the space. In fact, this is a vast generalization of Descartes’ idea of “taking graphs.” Given an algebraic equation, we can form a ring called the “residue ring” by a purely algebraic procedure, and the space associated with this residue ring recovers the graph of the algebraic equation (more precisely, the space is an algebraic variety, which is a geometric object that has richer information than the classical graph). Grothendieck established the above philosophy as a rigorous mathematical theory called the “scheme theory,” which rewrote the entire framework of classical algebraic geometry. His theory was developed on the basis of many methods and concepts from abstract mathematics developed in the 20th century, including categories and functors. 3.3 Arithmetic geometryThe main purpose of Grothendieck’s scheme theory was to apply the method of algebraic geometry to number theory. One of the ultimate goals of number theory is to understand the properties of the ring consisting of all integers. (It is a ring since the set of integers is closed under the addition, subtraction, and multiplication.) Thanks to the scheme theory, we can regard the ring of integers as the ring of functions on a space, hence can translate number-theoretic problems into geometric ones. The research field in which we study number theory using scheme theory is generally called “arithmetic geometry” (for more details about arithmetic geometry, see the article “Motives—Abstract Art of Numbers, Shapes, and Categories” in this issue [5]). Using the scheme theory, we can construct the theory of geometry on the basis of a system of non-intuitive numbers. For example, we often encounter a system of numbers in which 1 + 1 = 0 holds. Of course, this property does not hold in the world of real numbers. However, such a system of numbers is inevitable in the study of number theory, and even in many applications in science technologies. The scheme theory states that even in such a “strange” world of numbers, we can naturally consider nice geometry, making it possible to apply the method of algebraic geometry to information theory and cryptography. Algebraic geometry and arithmetic geometry stemmed from purely mathematical motivation and have been developed using many methods in abstract mathematics. However, surprisingly, they became a fountain of concrete applications in society. Arithmetic geometry developed closely with algebra, geometry, and analysis and became a mainstream of number theory. Interestingly, arithmetic geometry has provided many important concepts that have unexpected applications in different fields of science. For example, the theory of “weights,” which was a key to the proof of the Weil conjecture (an analogue of the Riemann hypothesis), became an essential basis of certain fields of theoretical physics, including string theory and mirror symmetry. The theory of elliptic curves, which played a fundamental role in the proof of the Fermat conjecture, has been widely used in constructing post-quantum cryptography. Arithmetic geometry is relatively young in the history of mathematics, and many innovations continue to occur. It will undoubtedly give us unexpected value in and outside mathematics in the next few centuries. 4. Representation theory and automorphic forms4.1 Group actionWhen mathematicians hear about representation theory, the first thing they think of is the action of a group on another object. When we think of groups, Évariste Galois, who died in a duel at the age of 20, comes to mind. He greatly simplified and generalized the proof of the Abel–Ruffini theorem, which states that “there is no formula for a general algebraic solution (a solution that can be expressed using the four arithmetic operations and roots) for equations of degree 5 or higher,” and used the forerunner of the group concept to characterize when a given equation has an algebraic solution. This theory is known today as Galois theory. Based on Galois theory is the monumental achievement in class field theory of Teiji Takagi, who studied under Frobenius in Berlin then under Hilbert and Klein in Göttingen at the turn of the 19th century, for actualizing “Kronecker’s dream of youth (Kronecker’s Jugendtraum)” based on Gauss’s law of quadratic reciprocity. It can also be said that Galois theory is the pillar of the magnificent theoretical system now known as the Langlands program (conjecture/philosophy), which is aimed at developing a non-commutative class field theory. However, the definition of a group is quite simple, it is a set such that 1) there is a binary operation called “multiplication” satisfying the associative law, 2) an identity element exists, and 3) each element has an inverse. Examples of finite groups are the familiar groups of symmetries of regular polyhedrons, the crystallographic point groups, symmetric groups that appear in the definitions of determinants, as well as general linear group GL(V), which is formed by regular (i.e., having the inverse) linear transformations on a finite-dimensional vector space V. The series of operations required to align the puzzle pieces on a Rubik’s Cube can also be thought of as physical group of operations performed by the “hand.” 4.2 Representation theory of groupsWhen we speak of representation theory, we are sometimes asked, “Do you mean literature or art? Or is there something like that in the field of mathematics?” It is influenced by expressionism, the art movement that originated in Germany in the early 20th century. It generally refers to the tendency to express emotions by reflecting them in works, as opposed to classical forms of representation*. Representation theory [11], in its most basic form, is the branch of mathematics that studies Vs on which elements of a group act as linear transformations of V (i.e., matrices, once a basis is fixed). Historically, the opportunity for representation theory to become an independent research subject was the letter from Dedekind to Frobenius in 1886 regarding the problem of factorization of the group determinants. This is the beginning of the character theory of finite groups. A character is the trace of a representation (of a matrix-valued function). In fact, a representation is essentially determined by its character. Sophus Lie also conducted research aimed at developing a Galois theory for differential equations and founded the current notion of Lie algebras and Lie groups. However, when it comes to these representations, it is indispensable to consider infinite dimensional Vs, in which case we need to consider the topology of the V. However, what decisively advanced the development of modern representation theory are the revolutionary theories in physics known as “relativity” and “quantum mechanics,” as well as the dramatic progress made in number theory on the road to the Langlands program. From a technical standpoint only, and although they vary somewhat depending on the algebraic system, representation theory can be summarized and broadly divided into the following three goals:
Some people may wonder why groups such as matrix groups, which already seem simple, must be expressed as difficult linear transformations on infinite dimensional spaces. However, the opposite is true. Even if something seems very complicated, if one unravels it correctly (decomposition), one will find that each part is simple (the action of an “easy” or “simple” group), thus one will be able to reach a true understanding of the object. These studies make full use of differential equations, functional analysis, the theory of special functions, combinatorics [12], and category theory, which has been well suited since Galois. 4.3 Automorphic formsThe Langlands program is often discussed purely in algebraic terms today, but the idea originated in Selberg’s theory of analytic continuation of non-holomorphic Eisenstein series and Harish-Chandra’s research on the representation theory of reductive Lie groups. In fact, representation theory is a strong bridge for solving questions in number theory that are formulated purely algebraically by replacing them with analytical notions such as Fourier transforms and q-series (via automorphic forms [13]). The natural actions of continuous and discrete groups are behind it, and the description of invariance with respect to these actions often clarifies the problems. For example, after Fermat’s Last Theorem, the Sato–Tate conjecture, which was considered to be many times more difficult, was (partially, i.e., a certain important class) solved by Richard Taylor and others in 2011. The Ramanujan conjecture, which led number theory in the 20th century, was that the absolute value distribution of the zeros of the L-function of an elliptic curve satisfies an analog of the Riemann hypothesis, but it was further formulated by Mikio Sato in 1963 that the argument (angle) distribution of the zeros follows a sin2-distribution. The difficulty lies in the fact that a problem that was solved with a single L-function in the Fermat conjecture must now be solved for an L-function associated with a representation determined by a symmetric product of n numbers (n = 1,2,3...). This solution is groundbreaking, but many more important issues remain unsolved. The challenge to the Sato–Tate conjecture is at the heart of the Langlands conjecture, and the solution awaits progress in non-holomorphic automorphic forms, which are deeply related to representation theory from the spectral viewpoint of invariant differential operators. The two articles in this issue on automorphic forms/representations [8] and representation theory [7] focus on research that goes to the core of this problem. The relationship between representation theory and quantum mechanics is deep and extends to number theory (e.g., [9]). It is also deeply connected to problems in invariant theory, combinatorics, special function’s theory, probability theory, and statistics (e.g., [6]). Some of these issues are introduced in the articles in this issue.
References
|
|||||||||||||||||||||||||||||